This is an important data structure. This data structure is used in many algorithms. The data structures that we have discussed in previous lectures are linear data structures. The linked list and stack are linear data structures. In these structures, the elements are in a line. We put and get elements in and from a stack in linear order. Queue is also a linear data structure as a line is developed in it. There are a number of applications where linear data structures are not appropriate. In such cases, there is need of some non-linear data structure. Some examples will show us that why non-linear data structures are important. Tree is one of the non-linear data structures.
Look at the following figure. This figure (11.1) is showing a genealogy tree of a family.
In this genealogy tree, the node at the top of the tree is Grand Parent i.e. the head of the family. There are three nodes under this one. These are children of Grand Parent. Then there are nodes under these three nodes i.e. the children of these three family members. You may have seen the tree like this of some other family. You can make the tree of your family too. The thing to be noted in this genealogical tree is that it is not a linear structure like linked list, in which we have to tell that who is the father and who is the son. We make it like a tree. We develop the tree top-down, in which the father of the family is on the top with their children downward. We can see the similar tree structure of a company. In the tree of a company, the CEO of the company is on the top, followed downward by the managers and assistant managers. This process goes downward according to the administrative hierarchy of the company. Our tree structure is different from the actual tree in the way that the actual tree grows from down to up. It has root downside and the leaves upside. The data structure tree is opposite to the real tree as it goes upside down. This top-down structure in computer science makes it easy to understand the tree data structure.
There may be situations where the data, in our programs or applications, is not in the linear order. There is a relationship between the data that cannot be captured by a linked list or other linear data structure. Here we need a data structure like tree.
In some applications, the searching in linear data structures is very tedious. Suppose we want to search a name in a telephone directory having 100000 entries. If this directory is in a linked list manner, we will have to traverse the list from the starting position. We have to traverse on average half of the directory if we find a name. We may not find the required name in the entire directory despite traversing the whole list. Thus it would be better to use a data structure so that the search operation does not take a lot of time. Taking into account such applications, we will now talk about a special tree data structure, known as binary tree.
Binary Tree
The mathematical definition of a binary tree is
“A binary tree is a finite set of elements that is either empty or is partitioned into three disjoint subsets. The first subset contains a single element called the root of the tree. The other two subsets are themselves binary trees called the left and right sub-trees”. Each element of a binary tree is called a node of the tree.
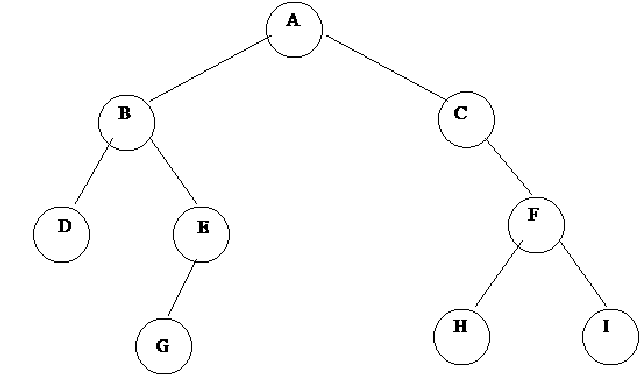
Following figure shows a binary tree.
 Fig 11.2: A Binary Tree |
There are nine nodes in the above figure of the binary tree. The nine nodes are A, B, C, D, E, F, G, H, and I. The node A is at the top of the tree. There are two lines from the node A to left and right sides towards node B and C respectively. Let’s have a look at the left side of the node A. There are also two lines from node B to left and right, leading to the nodes D and E. Then from node, E there is only one line that is to the left of the node and leads to node G. Similarly there is a line from node C towards the node F on right side of the node C. Then there are two lines from node F that leads to the nodes H and I on left and right side respectively.
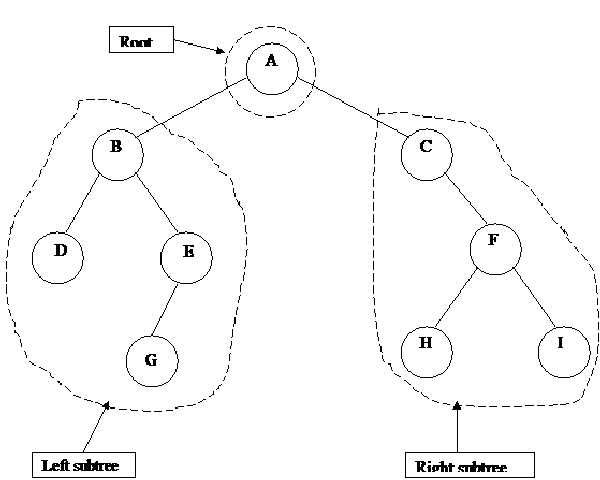
Now we analyze this tree according to the mathematical definition of the binary tree. The node A is the root of the tree. And tree structure (i.e. the nodes B, D, E, G and their relation) on the left side of the node A is a sub-tree, called the Left subtree. Similarly the nodes (C, F, H and I) on the right side of the node A comprise the sub-tree termed as Right subtree. Thus we made three parts of the tree. One part contains only one node i.e. A while the second part has all the nodes on left side of A, called as Left subtree. Similarly the third part is the Right subtree, containing the nodes on right side of A. The following figure depicts this scenario.
 Fig 11.3: Analysis of a binary tree |
The same process of sub classing the tree can be done at the second level. That means the left and right subtrees can also be divided into three parts similarly. Now consider the left subtree of node A. This left subtree is also a tree. The node B is the root of this tree and its left subtree is the node D. There is only one node in this left subtree. The right subtree of the node B consists of two nodes i.e. E and G. The following figure shows the analysis of the tree with root B.
 Fig 11.4: Analysis of a binary tree |
On going one step down and considering right subtree of node B, we see that E is the root and its left subtree is the single node G. There is no right subtree of node E or we can say that its right subtree is empty. This is shown in the following figure.
 Fig 11.5: Analysis of a binary tree |
Now the left sub tree of E is the single node G. This node G can be considered as the root node with empty left and right sub trees. The definition of tree is of recursive nature. This is due to the fact that we have seen that which definition has been applied to the tree having node A as root, is applied to its subtrees one level downward. Similarly as long as we go down ward in the tree the same definition is used at each level of the tree. And we see three parts i.e. root, left subtree and right subtree at each level.
Now if we carry out the same process on the right subtree of root node A, the node C will become the root of this right subtree of A. The left subtree of this root node C is empty. The right subtree of C is made up of three nodes F, H and I. This is shown in the figure below.
 Fig 11.6: Analysis of a binary tree |
Now we apply the same recursive definition on the level below the node C. Now the right subtree of the node C will be considered as a tree. The root of this tree is the node F. The left and right subtrees of this root F are the nodes H and I respectively.
The following figure depicts this.
 Fig 11.7: Analysis of a binary tree |
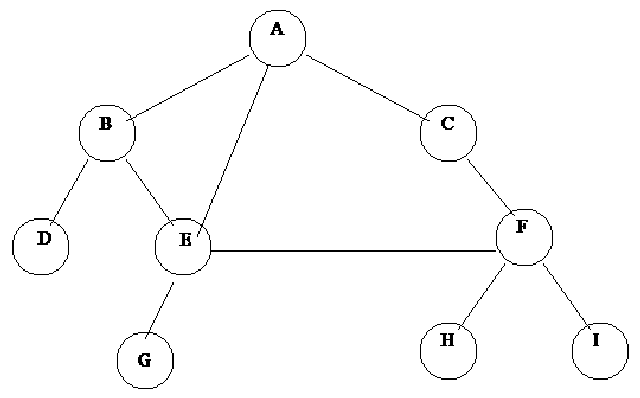
We make (draw) a tree by joining different nodes with lines. But we cannot join any nodes whichever we want to each other. Consider the following figure.
 Fig 11.8: A non-tree structure |
It is the same tree, made earlier with a little modification. In this figure we join the node G with D. Now this is not a tree. It is due to the reason that in a tree there is always one path to go (from root) to a node. But in this figure, there are two paths (tracks) to go to node G. One path is from node A to B, then B to D and D to G. That means the path is A-B-D-G. We can also reach to node G by the other path that is the path A-B-E-G. If we have such a figure, then it is not a tree. Rather, it may be a graph. We will discuss about graphs at the end of this course.
Similarly if we put an extra link between the nodes A and B, as in the figure below, then it is also no more a tree. This is a multiple graph as there are multiple (more than 1) links between node A and B.
 Fig 11.9: A non-tree structure |
Similarly if we put other links between different nodes, then the structure thus developed will not be a tree. The following figure is also an example of a structure that is not a tree as there are multiple links between the different nodes.
 Fig 11.10: A non-tree structure |
Terminologies of a binary tree
Now let’s discuss different terminologies of the binary tree. We will use these terminologies in our different algorithms. Consider the following figure.
 Fig 11.11: Terminologies used in a binary tree |
We have discussed that the node on the top is said root of the tree. If we consider the relationship of these nodes, A is the parent node with B and C as the left and right descendants respectively. C is the right descendant of A. Afterwards, we look at the node B where the node D is its left descendant and E is its right descendant. We can use the words descendant and child interchangeably. Now look at the nodes D, G, H and I. These nodes are said leaf nodes as there is no descendant of these nodes. We are just introducing the terminology here. In the algorithms, we can use the words root or parent, child or descendant. So the names never matter.
Strictly Binary Tree
There is a version of the binary tree, called strictly binary tree. A binary tree is said to be a strictly binary tree if every non-leaf node in a binary tree has non-empty left and right subtrees.
Now consider the previous figure 11.11. We know that a leaf node has no left or right child. Thus nodes D, G, H and I are the leaf nodes. The non-leaf nodes in this tree are A, B, C, E and F. Now according to the definition of strictly binary tree, these non-leaf nodes (i.e. A, B, C, E and F) must have left and right subtrees (Childs). The node A has left child B and right child C. The node B also has its left and right children that are D and E respectively. The non-leaf node C has right child F but not a left one. Now we add a left child of C that is node J. Here C also has its left and right children. The node F also has its left and right descendants, H and I respectively. Now the last non-leaf node E has its left child, G but no right one. We add a node K as the right child of the node E. Thus the tree becomes as shown below in the figure 11.12.
 Fig 11.12: A Strictly binary tree |
Now all the non-leaf nodes (A, B, C, E and F) have their left and right children so according to the definition, it is a strictly binary tree.
Level
The level of a node in a binary tree is defined as follows:
· Root has level 0,
· Level of any other node is one more than the level its parent (father).
· The depth of a binary tree is the maximum level of any leaf in the tree.
To understand level of a node, consider the following figure 11.13. This figure shows the same tree of figure 11.2, discussed so far.
 0 ---------------------------------------- Level 0 1 1 ------------------- Level 1 2 2 2 ------- Level 2 3 3 3 -Level 3 Fig 11.13: Level of nodes of a tree |
In the above figure, we have mentioned the level of each node. The figure also shows that the root node has level 0. We have talked in the definition of the level that the level of a node, other than root, is one more than the level of its parent. Now in the tree, the parent of nodes B and C is node A with level 0. Now by definition, the level of B and C will be 1 (i.e. level of A + 1). Now if go downward in the tree and see the nodes D, E and F, the parent node of D and E is B the level of which is 1. So the level of D and E is 2 (i.e. 1 + 1). Similarly the level of F is 2 as the level of its parent (i..e. C) is 1. In the same way, we can easily understand that the level of G, H and I is 3 as the parent nodes of these (E and F) have level 2. Thus we see that tree has multi levels in the downward direction. The levels of the tree increase, as the tree grows downward more. The number of nodes also increases.
Now let’s talk why we call it a binary tree. We have seen that each node has a maximum of two subtrees. There might be two, one or no subtree of a node. But it cannot have more than two. So, we call such a tree a binary one due to the fact that a node of it can have a maximum of two subtrees. There are trees whose nodes can have more than two subtrees. These are not binary trees. We will talk about these trees later.
By seeing the level of a tree, we can tell the depth of the tree. If we put level with each node of the binary tree, the depth of a binary tree is the maximum level. In the figure 11.13, the deepest node is at level 3 i.e. the maximum level is 3. So the depth of this binary tree is 3.
Complete Binary Tree
Now, if there are left and right subtrees for each node in the binary tree as shown below in figure 11.14, it becomes a complete binary tree.
 0 1 1 2 2 2 2 3 3 3 3 3 3 3 3 Fig 11.14: A Complete Binary Tree |
The definition of the complete binary tree is
“A complete binary tree of depth d is the strictly binary tree all of whose leaves are at level d”.
Now look at the tree, the leaf nodes of the tree are at level 3 and are H, I, J, K, L, M, N and O. There is no such a leaf node that is at some level other than the depth level d i.e. 3. All the leaf nodes of this tree are at level 3 (which is the depth of the tree i.e. d). So this is a complete binary tree. In the figure, all the nodes at level 3 are highlighted.
We know that the property of the binary tree is that its node can have a maximum of two subtrees, called as left and right subtrees. The nodes increase at each level, as the tree grows downward. In a complete binary tree, the nodes increase in a particular order. If we reconsider the previous tree (figure 11.14), we note that the number of node at level 0 is 1. We can say it 20, as 20 is equal to 1. Down to this, the node is the level 1 where the number of nodes is 2, which we can say 21, equal to 2. Now at the next level (i.e. level 2), the number of nodes is 4 that mean 22. Finally the number of nodes at level 3 is 8, which can be called as 23. This process is shown pictorially in the following figure 11.15.
 ------------- Level 0: 20 nodes ---------- Level 1: 21 nodes ---------- -------------- Level 2: 22 nodes ----------------- - ------------------------------------ Level 3: 23 nodes -------------------------------------------- Fig 11.15: Number of nodes at each level in a complete binary tree |
By observing the number of nodes at a particular level, we come to the conclusion that the number of nodes at a level is equal to the level number raising to the power of two. Thus we can say that in a complete binary tree at a particular level k, the number of nodes is equal to 2k. Note that this formula for the number of nodes is for a complete binary tree only. It is not necessary that every binary tree fulfill this criterion. Applying this formula to each level while going to the depth of the tree (i.e. d), we can calculate the total number of nodes in a complete binary tree of depth d by adding the number of nodes at each level. This can be written as the following summation.
20+ 21+ 22 + ……… + 2d = Sd j=0 2j = 2d+1 – 1
Thus according to this summation, the total number of nodes in a complete binary tree of depth d will be 2d+1 – 1. Thus if there is a complete binary tree of depth 4, the total number of nodes in it will be calculated by putting the value of d equal to 4. It will be calculated as under.
24+1 - 1 = 25 – 1 = 32 – 1 = 31
Thus the total number of nodes in the complete binary tree of depth 4 is 31.
We know that the total number of nodes (leaf and non-leaf) of a complete binary tree of depth d is equal to 2d+1 – 1. In a complete binary tree, all the leaf nodes are at the depth level d. So the number of nodes at level d will be 2d . These are the leaf nodes. Thus the difference of total number of nodes and number of leaf nodes will give us the number of non-leaf (inner) nodes. It will be (2d+1 – 1) – 2d i.e. 2d – 1. Thus we conclude that in a complete binary tree, there are 2d leaf nodes and 2d – 1 non-leaf (inner) nodes.
Level of a Complete Binary Tree
We can conclude some more results from the above mathematical expression. We can find the depth of a complete binary tree if we know the total number of nodes. If we have a complete binary tree with n total nodes, then by the equation of the total number of nodes we can write
Total number of nodes = 2d+1 – 1 = n
To find the value of d, we solve the above equation as under
2d+1 – 1 = n
2d+1 = n + 1
d + 1 = log2 (n + 1)
d = log2 (n + 1) – 1
After having n total nodes, we can find the depth d of the tree by the above equation. Suppose we have 100,000 nodes. It means that the value of n is 100,000, reflecting a depth i.e. d of the tree will be log2 (100000 + 1) – 1, which evaluates to 20. So the depth of the tree will be 20. In other words, the tree will be 20 levels deep. The significance of all this discussion about the properties of complete binary tree will become evident later.
Technorati Tags: ds tutorial,data structure tutorial,tree data structure,trees in data structure,tree ds,tree traversal data structure,tree types,types of trees,binary trees,binary search trees,bst,bst data structure,bst ds,complete binary search tree,non tree structure,linear tree,complete binary tree
No comments:
Post a Comment