Sorted Linked List implementation in C

include "stdio.h"
include "stdlib.h"
include "conio.h"



void del(int data);
void insert(int value);
void display();


struct node
{
    int data;
    struct node *link;
};

struct node *top=NULL,*temp, *temp1, *temp2, *temp3;

int main()
{
    int choice,data;

 
    while(1) //infinite loop is used to insert/delete infinite number of elements in linked list
    {
     
        printf("\n1.Insert\n2.Delete\n3.Display\n4.Exit\n");
        printf("\nEnter ur choice:");
        scanf("%d",&choice);
        switch(choice)
        {
        case 1:
         
         
            printf("Enter a new element :");
            scanf("%d",&data);
            insert(data);
            break;
         
        case 2:
     
        printf("Enter the value to be deleted from sorted linked list :");
            scanf("%d",&data);
         
            del(data);
            break;
         
        case 3:
            display();
            break;
        case 4:
            exit(0);
        }
     
    }  
getch();
return 0;
}

void insert(int data)
{

temp=(struct node *)malloc(sizeof(struct node));
temp->data=data;

if(top == NULL)
{

            temp->link=NULL;
            top=temp;
         
}
else            // top not null
{
temp1 = top ;
while(temp1 != NULL)
{
if(temp1->data >= data)   // list element is smaller ...

{
if(temp1 == top)   // list element is head ...
{
  temp->link = temp1;

top = temp;
break;

}
else // list element is not head ..
{

temp->link = temp1;
temp2->link = temp;
break;
}

}
else
{

if(temp1->link == NULL)
{
temp->link = NULL;
temp1->link = temp;
break;

}
else
{
temp2 = temp1;
temp1 = temp1->link;
}

}

}

}
          // creating a space for the new element.
                 
}

void del(int data)
{
     struct node *temp,*var;
     temp=top;
 int i=0;
     while(temp!=NULL)
     {
          if(temp->data == data)
          {      i = 1;   // Flag ..
                if(temp==top)
                {
                     top=temp->link;
                     free(temp);
                   break;
                }
                else
                {
                     var->link=temp->link;
                     free(temp);
                     break;
                 
                }
          }
          else
          {
               var=temp;
               temp=temp->link;
          }
     }
     if(i == 1)
     {
printf("data deleted from list is %d",data);
 
     }
     else
     {
      printf("\n The required data, %d is not found in the list. go look somewhere else",data);

     }
}





void display()
{
         temp=top;
            if(temp==NULL)
            {
                printf("\nStack is empty\n");
            }
         
            while(temp!=NULL)
            {
                printf(" %d ->",temp->data);
                temp=temp->link;
            }
             
}

Priority Queue Implementation in C using Arrays

#include <stdio.h>

#include <conio.h>

#define size 5

int queue[5][2] = {0};

int top = -1;

int bottom;

void push(int value, int pr)

{

int i,j,k;

if(top < size-1)

{

if(queue[top][1] > pr)

{

for(i=0;i<top;i++)

{

if(queue[i][1] > pr)

{

break;

}

}

for(j=top;j>=i;j--)

{

queue[j+1][0] = queue[j][0];

queue[j+1][1] = queue[j][1];

}

top++;

queue[i][0] = value;

queue[i][1] = pr;

}

else

{

top++;

queue[top][0] = value;

queue[top][1] = pr;

}

}

else

{

printf("queue overflow \n");

}

}

void pop()

{

int i;

if(queue[0][0] == 0)

{

printf("\n The queue is empty  \n");

}

else

{

printf("After , dequeue the following value is erased \n  %d \n", queue[0][0]);

for(i=0;i<top;i++)

{

queue[i][0] = queue[i+1][0];

queue[i][1] = queue[i+1][1];

}

queue[top][0] = 0;

queue[top][1] = 0;

top--;

}

}

void display()

{ int i,j;

printf("Element\tPriority \n");

for(i=size - 1;i>=0;i--)

{

for(j=0;j<2;j++)

{

printf(" %d\t",queue[i][j]);

}

printf("\n");

}

}

int main()

{

int i,j, ch=0 ,value = 0,pr=0;

while(1)

{

printf("\n Please Enter the choice. \n");

printf("1 for Enqueue \n 2 for Dequeue \n 3 for display\n  5 for exit: \t \n");

scanf("%d",&ch);

switch(ch)

{

case 1:

printf("\n Please Enter the number to be inserted: \t ");

scanf("%d", &value);

printf("\n Please Enter the priority: \t ");

scanf("%d", &pr);

push(value,pr);

break;

case 2:

pop();

break;

case 3:

display();

break;

case 5:

exit(0);

default:

printf("You entered wrong choice\n");

}

}

}

C program for Stack implementation using array

#include "stdio.h"
#include "conio.h"

#define size 5

int stack[size] = {0};

int top = -1;

void push(int value)
{
if(top < size)
{
top++;
stack[top] = value;
}
else
{
printf("Stack overflow \n");
}
}

void pop()
{
if(top >= 0)
{
printf("The popped element is:\t %d \n", stack[top]);
stack[top] = 0;
top--;
}

else
{
printf("Stack underflow \n");
}


}
void display()
{

                 int i;

for(i=size - 1;i>=0;i--)
{
printf(" %d \n",stack[i]);
}
}

void tos()
{
printf("The value at top is %d", stack[top]);
}

int main()
{

int i,j, ch=0 ,value = 0;

while(1)
{
printf("\n Please Enter the choice. \n");
printf("1 for push\n 2 for pop \n 3 for display\n 4 for top \t  \n 5 for exit");
scanf("%d",&ch);

switch(ch)
{
case 1:
printf("\n Please Enter the number to be inserted: \t");
scanf("%d", &value);
push(value);
break;

case 2:

pop();

break;

case 3:

display();

break;


case 4:
tos();

break;

case 5:

exit(0);



}
}

}

Quick Sort

 

Quicksort is another divide and conquer algorithm. Quicksort is based on the idea of partitioning (splitting) the list around a pivot or split value. Quicksort is also a divide and conquer algorithm. We see pictorially, how the quick sort algorithm works. Suppose we have an array as shown in the figure Fig 45.33.

We select an element from the array and call it the pivot. In this array, the pivot is the middle element 5 of the array. Now, we swap this with the last element 3 of the array. The updated figure of the array is shown in Fig 45.34.

As shown in Fig 45.34, we used two indexes low and high. The index low is started from 0^th position of the array and goes towards right until n-1^th position. Inside this loop, an element that is bigger than the pivot is searched. The low index is incremented further as 4 is less than 5.

low is pointing to element 12 and it is stopped here as 12 is greater than 5. Now, we start from the other end, the high index is moved towards left from n-1^th position to 0. While coming from right to left, we search such an element that is smaller than 5. Elements 7 and 11 towards left are greater than 5, therefore, the high pointer is advanced further towards left. high index is stopped at the next position as next element 2 is smaller than 5. Following figure Fig 45.36 depicts the latest situation.

Divide and Conquer

We had started discussing three new sorting algorithms; merge sort, quick sort and heap sort. All of these three algorithms take time proportional to nlog₂n. Our elementary three sorting algorithms were taking n² time; therefore, these new algorithms with nlog₂n time are faster. In search operation, we were trying to reduce the time from n to log₂n.

Let’s discuss these sorting algorithms; merge sort, quick sort and heap sort in detail.

We had started our discussion from divide and conquer rule where we also saw an example. Instead of sorting a whole array, we will divide it in two parts, each part is sorted separately and then they are merged into a single array.

Let’ see few analysis to confirm the usefulness of the divide and conquer technique.

- To sort the halves approximate time is (n/2)2+(n/2)2

- To merge the two halves approximate time is n

- So, for n=100, divide and conquer takes approximately:

= (100/2)2 + (100/2)2 + 100

= 2500 + 2500 + 100

= 5100 (n2 = 10,000)

Comparison of Complexity of Algorithms

We have studied these three algorithms i.e. selection sort, insertion sort and bubble sort. Now considering the above three algorithms, we see that these algorithms are easy to understand. Coding for these algorithms is also easy. These three algorithms are in place algorithms. There is no need of extra storage for sorting an array by these algorithms. With respect to the time complexity, these algorithms are proportional to N². Here N is the number of elements. So we can see that as the value of N increases, the performance time of these algorithms increases considerably as it is proportional to N². Thus these algorithms are expensive with respect to time performance. There are algorithms that have the time complexity proportional to N log₂ (N). The following table shows the respective values of N² and N log₂(N) for some values of N.

N	N2	N Log2 (N)
10	100	33.21
100	10000	664.38
1000	1000000	9965.78
10000	100000000	132877.12
100000	10000000000	1660964.04
1000000	1E+12	19931568.57

From this table we can see that for a particular value of N, the value of N² is very large as compared to the value of N log₂ (N). Thus we see that the algorithms whose time complexity is proportional to N² are much time consuming as compared to the algorithms the time complexity of which is proportional to N log₂ (N). Thus we see that the N log₂ (N) algorithms are better than the N² algorithms.

N log₂ (N) Algorithms

Now let’s see the algorithms that are N log₂ (N) algorithms. These include the following algorithms.

• Merge Sort
• Quick Sort
• Heap Sort

These three algorithms fall under ‘divide and conquer category’. The divide and conquer strategy is well known in wars. The philosophy of this strategy is ,’ divide your enemy into parts and then conquer these parts’. To conquer these parts is easy, as these parts cannot resist or react like a big united enemy. The same philosophy is applied in the above algorithms. To understand the divide and conquer strategy in sorting algorithm, let’s consider an example. Suppose we have an unsorted array of numbers is given below.

Bubble Sort

The third sorting algorithm is bubble sort. The basic idea of this algorithm is that we bring the smaller elements upward in the array step by step and as a result, the larger elements go downward. If we think about array as a vertical one, we do bubble sort. The smaller elements come upward and the larger elements go downward in the array. Thus it seems a bubbling phenomenon. Due to this bubbling nature, this is called the bubble sort. Thus the basic idea is that the lighter bubbles (smaller numbers) rise to the top. This is for the sorting in ascending order. We can do this in the reverse order for the descending order.

The steps in the bubble sort can be described as below

• Exchange neighboring items until the largest item reaches the end of the array

• Repeat the above step for the rest of the array

In this sort algorithm, we do not search the array for the smallest number like in the other two algorithms. Also we do not insert the element by shifting the other elements. In this algorithm, we do pair-wise swapping. We will take first the elements and swap the smaller with the larger number. Then we do the swap between the next pair. By repeating this process, the larger number will be going to the end of the array and smaller elements come to the start of the array.

Insertion Sort

The main idea of insertion sort is

• Start by considering the first two elements of the array data. If found out of order, swap them

• Consider the third element; insert it into the proper position among the first three elements.

• Consider the fourth element; insert it into the proper position among the first four elements.

• … …

This algorithm is not something uncommon to the persons who know card playing. In the game of cards, a player gets 13 cards. He keeps them in the sorted order in his hand for his ease. A player looks at the first two cards, sorts them and keeps the smaller card first and then the second. Suppose that two cards were 9 and 8, the player swap them and keep 8 before 9. Now he takes the third card. Suppose, it is 10, then it is in its position. If this card is of number 2, the player will pick it up and put it on the start of the cards. Then he looks at the fourth card and inserts it in the first three cards (that he has sorted) at a proper place. He repeats the same process with all the cards and finally gets the cards in a sorted order. Thus in this algorithm, we keep the left part of the array sorted and take element from the right and insert it in the left part at its proper place. Due to this process of insertion, it is called insertion sorting.

Selection Sort

 

Suppose we have an array with different numbers. For sorting it in an ascending order, selection sorting will be applied on it in the following manner. We find the smallest number in the array and bring it to the position 1. We do the same process with the remaining part of the array and bring the smallest number among the remaining array to the next position. This process continues till the time all the positions of the array are filled with the elements. Thus the main idea of selection sort is that

• find the smallest element

• put it in the first position

• find the next smallest element in the remaining elements

• put it in the second position

• …

• And so on, until we get to the end of the array

Let’s understand this algorithm by considering an example with the help of figures.

Consider an array that has four numbers i.e. 19, 5, 7 and 12 respectively. Now we want to sort this array in ascending order. To sort the array, selection algorithm will be applied on it.

Binary Search

 

The binary search is an algorithm of searching, used with the sorted data. As we have sorted elements in the array, binary search method can be employed to find data in the array. The binary search finds an element in the sorted array in log n time. If we have 100000 elements in the array, the log 1000000 will be 20 i.e. very small as compared to 100000. Thus binary search is very fast.

The binary search is like looking up a phone number in the directory or looking up a word in the dictionary. For looking a word in the dictionary, we start from the middle in the dictionary. If the word that we are looking for comes before words on the page, it shows that the word should be before this page. So we look in the first half. Otherwise, we search for the word in the second half of the dictionary. Suppose the word is in the first half of the dictionary, we consider first half for looking the word. We have no need to look into the second half of the dictionary. Thus the data to be searched becomes half in a step. Now we divide this portion into two halves and look for the word. Here we again come to know that the word is in the first half or in the second half of this portion. The same step is repeated with the part that contains the required word. Finally, we come to the page where the required word exists. We see that in the binary search, the data to be searched becomes half in each step. And we find the entry very fast. The number of maximum steps needed to find an entry is log n, where n is the total number of entries. Now if we have 100000 entries, the maximum number of attempts (steps) required to find out the entry will be 20 (i.e. log 1000000).

If already sorted data is available, then it is better to apply an algorithm of binary search for finding some item inside instead of searching from start to the end in sequence. The application of this algorithm will help get the results very quickly.

Complete Binary Tree

We have earlier discussed the properties of the binary trees besides talking about the internal and external nodes’ theorem. Now we will discuss another property of binary trees that is related to its storage before dilating upon the complete binary tree and the heap abstract data type.

Here is the definition of a complete binary tree:

• A complete binary tree is a tree that is completely filled, with the possible exception of the bottom level.
• The bottom level is filled from left to right.

A binary tree T with n levels is complete if all levels except possibly the last are completely full,
and the last level has all its nodes to the left side.You may find the definition of complete binary tree in the books little bit different from this. A perfectly complete binary tree has all the leaf nodes. In the complete binary tree, all the nodes have left and right child nodes except the bottom level. At the bottom level, you will find the nodes from left to right. The bottom level may not be completely filled, depicting that the tree is not a perfectly complete one. Let’s see a complete binary tree in the figure below:

In the above tree, we have nodes as A, B, C, D, E, F, G, H, I, J. The node D has two children at the lowest level whereas node E has only left child at the lowest level that is J. The right child of the node E is missing. Similarly node F and G also lack child nodes. This is a complete binary tree according to the definition given above. At the lowest level, leaf nodes are present from left to right but all the inner nodes have both children. Let’s recap some of the properties of complete binary tree.

• A complete binary tree of height h has between 2^h to 2^h+1 –1 nodes.

• The height of such a tree is log₂N where N is the number of nodes in the tree.

• Because the tree is so regular, it can be stored in an array. No pointers are necessary.

We have taken the floor of the log₂ N. If the answer is not an integer, we will take the next smaller integer. So far, we have been using the pointers for the implementation of trees. The treeNode class has left and right pointers. We have pointers in the balance tree also. In the threaded trees, these pointers were used in a different way. But now we can say that an array can be stored in a complete binary tree without needing the help of any pointer.

Now we will try to remember the characteristics of the tree. 1) The data element can be numbers, strings, name or some other data type. The information is stored in the node. We may retrieve, change or delete it. 2) We link these nodes in a special way i.e. a node can have left or right subtree or both. Now we will see why the pointers are being used. We just started using these. If we have some other structure in which trees can be stored and information may be searched, then these may be used. There should be reason for choosing that structure or pointer for the manipulation of the trees. If we have a complete binary tree, it can be stored in an array easily.

The following example can help understand this process. Consider the above tree again.

We have seen an array of size 15 in which the data elements A, B, C, D, E, F, G, H, I, J have been stored, starting from position 1. The question arises why we have stored the data element this way and what is justification of storing the element at the 1^st position of the array instead of 0^th position? You will get the answers of these very shortly.

The root node of this tree is A and the left and right children of A are B and C. Now look at the array. While storing elements in the array, we follow a rule given below:

• For any array element at position i, the left child is at 2i, the right child is at (2i +1) and the parent is at floor(i/2).

In the tree, we have links between the parent node and the children nodes. In case of having a node with left and right children, stored at position i in the array, the left child will be at position 2i and the right child will be at 2i+1 position. If the value of i is 2, the parent will be at position 2 and the left child will be at position 2i i.e. 4 .The right child will be at position 2i+1 i.e. 5. You must be aware that we have not started from the 0^th position. It is simply due to the fact if the position is 0, 2i will also become 0. So we will start from the 1^st position, ignoring the 0^th.

Lets see this formula on the above array. We have A at the first position and it has two children B and C. According to the formula the B will be at the 2i i.e. 2^nd position and C will be at 2i+1 i.e. 3^rd position. Take the 2^nd element i.e. B, it has two children D and E. The position of B is 2 i.e. the value of i is 2. Its left child D will be at positon 2i i.e. 4^th position and its right child E will be at position 2i+1 i.e. 5. This is shown in the figure below:

If we want to keep the tree’s data in the array, the children of B should be at the position 4 and 5. This is true. We can apply this formula on the remaining nodes also. Now you have understood how to store tree’s data in an array. In one respect, we are using pointers here. These are not C++ pointers. In other words, we have implicit pointers in the array. These pointers are hidden. With the help of the formula, we can obtain the left and right children of the nodes i.e. if the node is at the ith position, its children will be at 2i and 2i+1 position. Let’s see the position of other nodes in the array.

As the node C is at position 3, its children should be at 2*3 i.e. 6^th position and 2*3+1 i.e. 7^th position. The children of C are F and G which should be at 6^th and 7^th position. Look at the node D. It is at position 4. Its children should be at position 8 and 9. E is at position 5 so its children should be at 10 and 11 positions. All the nodes have been stored in the array. As the node E does not have a right child, the position 11 is empty in the array.

You can see that there is only one array going out of E. There is a link between the parent node and the child node. In this array, we can find the children of a node with the help of the formula i.e. if the parent node is at ith position, its children will be at 2i and 2i+1 position. Similarly there is a link between the child and the parent. A child can get its parent with the help of formula i.e. if a node is at ith position, its parent will be at floor(i/2) position. Let’s check this fact in our sample tree. See the diagram below:

Level Order Numbers & Array index

Consider the node J at position is 10. According to the formula, its parent should be at floor(10/2) i.e. 5 which is true. As the node I is at position 9, its parent should be at floor(9/2) i.e. 4. The result of 9/2 is 4.5. But due to the floor, we will round it down and the result will be 4. We can see that the parent of I is D which is at position 4. Similarly the parent of H will be at floor(8/2). It means that it will be at 4. Thus we see that D is its parent. The links shown in the figure depict that D has two children H and I. We can easily prove this formula for the other nodes.

From the above discussion we note three things. 1) We have a complete binary tree, which stores some information. It may or may not be a binary search tree. This tree can be stored in an array. We use 2i and 2i+1 indexing scheme to put the nodes in the array. Now we can apply the algorithms of tree structure on this array structure, if needed.

Now let’s talk about the usage of pointers and array. We have read that while implementing data structures, the use of array makes it easy and fast to add and remove data from arrays. In an array, we can directly locate a required position with the help of a single index, where we want to add or remove data. Array is so important that it is a part of the language. Whereas the data structures like tree, stack and queue are not the part of C or C++ language as a language construct. However we can write our classes for these data structures. As these data structures are not a part of the language, a programmer can not declare them directly. We can not declare a tree or a stack in a program. Whereas we can declare an array directly as int x []; The array data type is so efficient and is of so common use that most of the languages support it. The compiler of a language handles the array and the programmer has to do nothing for declaring and using an array.

We have built the binary trees with pointers. The use of pointers in the memory requires some time. In compilers or operating system course, we will read that when a program is stored in the memory and becomes a process, the executable code does not come in the memory. There is a term paging or virtual memory. When a program executes, some part of it comes in the memory. If we are using pointers to go to different parts of the program, some part of the code of program will be coming (loading) to memory while some other may be removed (unloading) from the memory. This loading and unloading of program code is executed by a mechanism, called paging. In Windows operating system, for this virtual memory (paging mechanism), a file is used, called page file. With the use of pointers, this process of paging may increase. Due to this, the program may execute slowly. In the course of Operating System and Compilers, you will read in detail that the usage of pointers can cause many problems.

So we should use arrays where ever it can fulfill our requirements. The array is a very fast and efficient data structure and is supported by the compiler. There are some situations where the use of pointers is beneficial. The balancing of AVL tree is an example in this regard. Here pointers are more efficient. If we are using array, there will be need of moving a large data here and there to balance the tree.

From the discussion on use of pointers and array, we conclude that the use of array should be made whenever it is required. Now it is clear that binary tree is an important data structure. Now we see that whether we can store it in an array or not. We can surely use the array. The functions of tree are possible with help of array. Now consider the previous example of binary tree. In this tree, the order of the nodes that we maintained was for the indexing purpose of the array. Moreover we know the level-order traversal of the tree. We used queue for the level-order of a tree. If we do level-order traversal of the tree, the order of nodes visited is shown with numbers in the following figure.

In the above figure, we see that the number of node A is 1. The node B is on number 2 and C is on number 3. At the next level, the number of nodes D, E, F and G are 4, 5, 6 and 7 respectively. At the lowest level, the numbers 8, 9 and 10 are written with nodes H, I and J respectively. This is the level-order traversal. You must remember that in the example where we did the preorder, inorder and post order traversal with recursion by using stack. We can do the level-order traversal by using a queue. Now after the level-order traversal, let’s look at the array shown in the lower portion of the above figure. In this array, we see that the numbers of A, B, C and other nodes are the same as in the level-order traversal. Thus, if we use the numbers of level-order traversal as index, the values are precisely stored at that numbers in the array. It is easy for us to store a given tree in an array. We simply traverse the tree by level-order and use the order number of nodes as index to store the values of nodes in the array. A programmer can do the level-order traversal with queue as we had carried out in an example before. We preserve the number of nodes in the queue before traversing the queue for nodes and putting the nodes in the array. We do not carry out this process, as it is unnecessarily long and very time consuming. However, we see that the level-order traversal directly gives us the index of the array depending upon which data can be stored.

Now the question arises if we can store the binary tree in an array, why there should be the use of pointers? It is very simple that an array is used when the tree is a complete binary tree. Array can also be used for the trees that are not complete binary trees. But there will be a problem in this case. The size of the array will be with respect to the deepest level of the tree according to the traversal order. Due to incomplete binary tree, there will be holes in the array that means that there will be some positions in the array with no value of data. We can understand it with a simple example. Look at the following figure where we store a complete binary tree in an array by using 2i and 2i+1 scheme. Here we stored the nodes from A to J in the array at index 1 to 10 respectively.

Suppose that this tree is not complete. In other words, B has no right subtree that means E and J are not there. Similarly we suppose that there is no right subtree of A. Now the tree will be in the form as shown in the following figure (29.2).

In this case, the effort to store this tree in the array will be of no use as the 2i and 2i+1 scheme cannot be applied to it. To store this tree, it may be supposed that there are nodes at the positions of C, F, G, E and J (that were there in previous figure). Thus we transform it into a complete binary tree. Now we store the tree in the array by using 2i and 2i +1 scheme. Afterwards, the data is removed from the array at the positions of the imaginary nodes (in this example, the nodes are C, F, G, E and J). Thus we notice that the nodes A, B and H etc are at the positions, depicting the presence of a complete binary tree. The locations of C, f, G, E and J in the array are empty as shown in the following figure.

Now imagine that an incomplete binary tree is very deep. We can store this tree in the array that needs to be of large size. There will be holes in the array. This is the wastage of memory. Due to this reason, it is thought that if a tree is not completely binary, it is not good to store it into an array. Rather, a programmer will prefer to use pointers for the storage.

Remember that two things are kept into view while constructing a data structure that is memory and time. There should such a data structure that could ensure the running of the programs in a fast manner. Secondly, a data structure should not use a lot of memory so that a large part of memory occupied by it does not go waste. To manage the memory in an efficient way, we use dynamic memory with the help of pointers. With the use of pointers only the required amount of memory is occupied.

We also use pointers for complex operations with data structure as witnessed in the deletion operation in AVL tree. One of the problems with arrays is that the memory becomes useless in case of too many empty positions in the array. We cannot free it and use in other programs as the memory of an array is contiguous. It is difficult to free the memory of locations from 50 to 100 in an array of 200 locations. To manage the memory in a better way, we have to use pointers.

Technorati Tags: ds tutorial,data structure tutorial,tree data structure,trees in data structure,tree ds,tree traversal data structure,tree types,types of trees,binary trees,binary search trees,bst,bst data structure,bst ds,complete binary search tree,non tree structure,linear tree,complete binary tree

Properties of Binary Tree

 

There is a relationship between internal nodes and external nodes i.e. If the number of internal nodes is N, the number of external nodes will be N+1. Let us discuss another property of the binary trees.

Property

A binary tree with N internal nodes has 2N links, N-1 links to internal nodes and N+1 links to external nodes.

Please recall that the first property dealt with the relationship between internal and external nodes. This property is dealing with the relationship of links to the internal nodes.

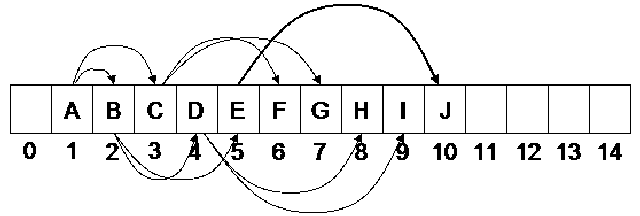
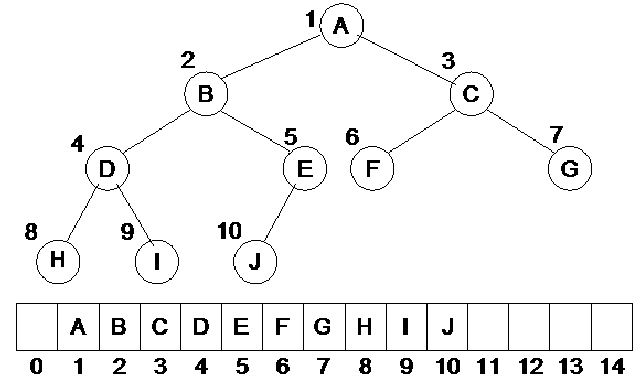
Now, what is a link? As you might already have understood, a link is that line, which we draw between two nodes in a tree. Internally we use pointers in C++ to realize links. In pictorial sketches, however, we use a line to show a link between the two nodes. The property defines, that if you have a binary tree with Nodes, how many links, it will have between the internal nodes (remember, it includes the leaf nodes), and how many links it will have between the external nodes. We have not been showing any links between the external nodes in the diagrams. These are, in fact, null pointers. That means, these are the links, which we will show with the help of the square nodes. Let us see a binary tree, on the basis of which, we will further explore this property. In the following figure, the binary tree is shown again, which, in addition to the normal links between the internal nodes, also contains external nodes as squares and the external links as lines going to those squares.

Now if you count the total number of links in the diagram between internal and external nodes, it will be 2N. Remember, we are talking about links and not nodes. In this tree, we have 9 nodes marked with capital letters, 8 internal links and 10 external links. Adding the both kinds of links, we get 18, which is exactly 2 x 9.

As discussed already that these properties are mathematical theorems and can therefore be proven mathematically. Let us now prove this property as to how do we get 2N links in a binary tree with N internal nodes.

Property

A binary tree with N internal nodes has 2N links, N-1 links to internal nodes and N+1 links to external nodes.

- In every rooted tree, each node, except the root, has a unique parent.

- Every link connects a node to its parents, so there are N-1 links connecting internal nodes.

- Similarly each of the N+1 external nodes has one link to its parents.

- Thus N-1+N+1=2N links.

In the previous lectures, I told you about the important property of the trees, that they contain only one link between the two nodes. I had also shown you some structures, which did not follow this property and I told you, that those were graphs.

Threaded Binary Trees

- In many applications binary tree traversals are carried out repeatedly.

- The overhead of stack operations during recursive calls can be costly.

- The same would true if we use a non-recursive but stack-driven traversal procedure

- It would be useful to modify the tree data structure which represents the binary tree so as to speed up, say, the inorder traversal process: make it "stack-free".

You must be remembering that there were four traversing methods of binary trees: preorder, inorder,

postorder and levelorder. First three preorder, inorder and postorder were implemented using recursion. Those recursive routines were very small, 3 to 4 lines of code and they could be employed to traverse a tree of any size.

We also traversed BST in inorder to retrieve the information in sorted order. We employed stacks in recursive implementations. Although, recursive routines are of few lines but when recursion is in action, recursive stack is formed that contains the function calls. We also explicitly used stack for inorder non-recursive traversal. When the calling pattern of recursive and non-recursive stack based routines were compared, the calling pattern of both of the routines were similar.

Suppose that we have a BST that is traversed again and again for some operations of find or print. Due to lot of recursive operations, the stack size keeps on growing. As a result, the performance is affected. To overcome this performance bottleneck, we can use non-recursive method but stack-driven traversal will again be an issue. The push and pop operations of stack for insertion and retrieval will again take time. So is there a way to do traversal without using a stack neither of implicit function call stack nor explicit. The same idea is presented in the last bullets above that leads to threaded binary trees:

- It would be useful to modify the tree data structure which represents the binary tree so as to speed up, say, the inorder traversal process: make it "stack-free".

The idea in the above statement is to modify the tree data structure to speed up and make it stack-free. Now, we see what kind of modification is required in the binary trees.

- Oddly, most of the pointer fields in our representation of binary trees are NULL!

- Since every node (except the root) is pointed to, there are only N-1 non-NULL pointers out of a possible 2N (for an N node tree), so that N+1 pointers are NULL.

We know that all the leaf node pointers are NULL. Each node of the tree contains the data part, two pointer variables for left and right nodes links. But these pointer variables are used when the node has further child nodes. We know that in a binary tree the total number of links are 2N including both internal and external and the number of NULL pointers is N+1.

In the figure above, the tree is the same as shown in Fig 27.1. The square nodes shown in this figure are external nodes. Thinking in terms of pointers all the pointers of these nodes are NULL or in other words they are available to be used later. We recognize these nodes as leaf nodes. Besides that, what can we achieve using them is going to be covered in Threaded Binary Trees.

- The threaded tree data structure will replace these NULL pointers with pointers to the inorder successor (predecessor) of a node as appropriate.

We are creating a new data structure inside the tree and when the tree will be constructed, it will be called a threaded binary tree. The NULL pointers are replaced by the inorder successor or predecessor. That means while visiting a node, we can tell which nodes will be printed before and after that node.

- We'll need to know whenever formerly NULL pointers have been replaced by non NULL pointers to successor/predecessor nodes, since otherwise there's no way to distinguish those pointers from the customary pointers to children.

This is an important point as we need to modify our previous logic of identifying leaf nodes. Previously the node with left and right nodes as NULL was considered as the leaf node but after this change the leaf node will contain pointers to predecessor and successor. So in order to identify that the pointers has been modified to point to their inorder successor and predecessor, two flags will be required in the node. One flag will be used for successor and other for predecessor. If both the pointers were NULL, left pointer variable will be used to point inorder predecessor, the flag for this will be turned on and the right pointer variable will be used to keep inorder successor and the flag will be turned on once the successor address is assigned.

Adding Threads During Insert

If we print the above tree in inorder we will get the following output:

14 15 18 20

In the above figure, the node 14 contains both left and right links. The left pointer is pointing to a subtree while the right subtree is pointing to the node 15. The node 15’s right link is towards 18 but the left link is NULL but we have indicated it with a rounded dotted line towards 14. This indicates that the left pointer points to the predecessor of the node.

Below is the code snippet for this logic.

t->L = p->L; // copy the thread
t->LTH = thread;
t->R = p; // *p is successor of *t
t->RTH = thread;

p->L = t; // attach the new leaf
p->LTH = child;

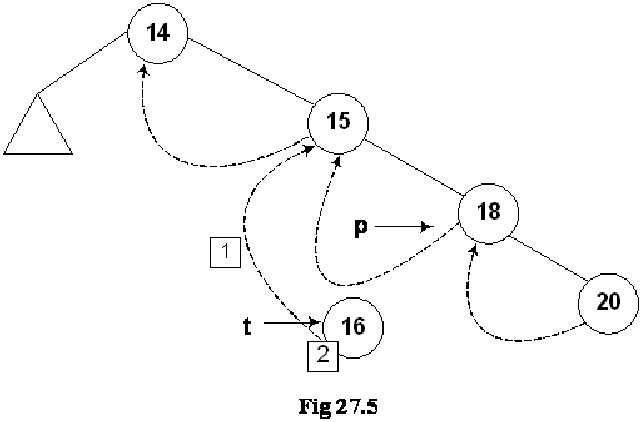
Let’s insert a new node in the tree shown in the above figure. The Fig 27.4 indicates this new insertion.

The new node 16 is shown in the tree. The left and right pointers of this new node are NULL. As node 16 has been created, it should be pointed to by some variable. The name of that variable is t. Next, we see the location in the tree where this new node with number 16 can be inserted. Clearly this will be after the node 15 but before node 18. As a first step to insert this node in the tree as the left child of the node 18, we did the following:

1. t->L = p->L; // copy the thread
2. t->LTH = thread;
3. t->R = p; // *p is successor of *t
4. t->RTH = thread;

5. p->L = t; // attach the new leaf
6. p->LTH = child;

As the current predecessor of node 18 is 15. After node 16 will be inserted in the tree, it will become the inorder predecessor of 18, therefore, in the first line of the code t->L = p->L, left pointer of node 18 (pointed to by pointer p) is assigned to the left pointer of node 16 (pointer to by pointer t).

In the next line of code t->LTH = thread, the left flag is assigned a variable thread that is used to indicate that it is on.

In the third line of code, t->R = p, 18 being the successor of node 18, its pointer p is assigned to the right pointer (t->R) of node 16.

Next line, t->RTH = thread contains flag turning on code.

In the next line p->L = t, the node 16 is attached as the left child of the node 18.

The flag is truned on in the last line, p->LTH = child.

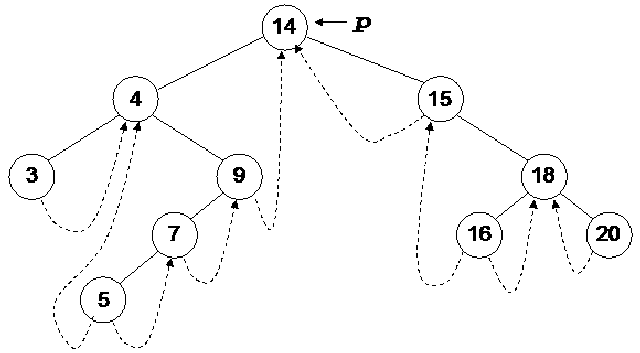
If we insert few more nodes in the tree, we have the tree as given below:

Above given is a BST and you have seen many BSTs before, which are not thread binary trees. Without the threads, it is clear from the figure that there are number of links present in the tree that are NULL. We have converted the NULLs to threads in this tree.

Let’s do inorder non-recursive traversal of the tree. We started at 14 then following the left link came to 4 and after it to 3. If we use recursion then after the call for node 3 is finished (after printing 3), it returns to node 4 call and then 4 is printed using the recursive call stack. Here we will print 3 but will not stop. As we have used threads, we see the right pointer of node 3 that is not NULL and pointing to its successor node 4, we go to 4 and print it. Now which node is inorder successor of node 4. It is node 5.

From node 4, we traversed to right child of it node 9. From node 9, we went to node 7 and then finally node 5. Now, this node 5 is a leaf node. Previously, without using threads, we could identify leaf nodes, whose both pointers left and right were NULL. In this case, using threads, as discussed above, we set the pointers and turn the flags on when a pointer left or right is set to its predecessor or successor. After printing node 5, we traverse its right thread and go to node 7. In this fashion, whole of the tree can be traversed without recursion.

Now, let’s see some code:

TreeNode* nextInorder(TreeNode* p)

{

if(p->RTH == thread)

return(p->R);

else {

p = p->R;

while(p->LTH == child)

p = p->L;

return p;

}

}

Above given is a routine nextInorder, which gives the inorder

successor of a node passed in parameter pointer p. Now what it does is:

If the RTH flag of the p node (the node passed in the parameter) is thread then it will return the node being pointed by the right thread (p->R), which would be its inorder successor. Otherwise, it does the following.

It goes to the right node of p and starts pointing it using the same p pointer. From there it keeps on moving (in a loop fashion) towards the left of the node as long as the statement p->LTH == child is true. After this loop is terminated, the node p is returned.

Next, we see this pictorially.

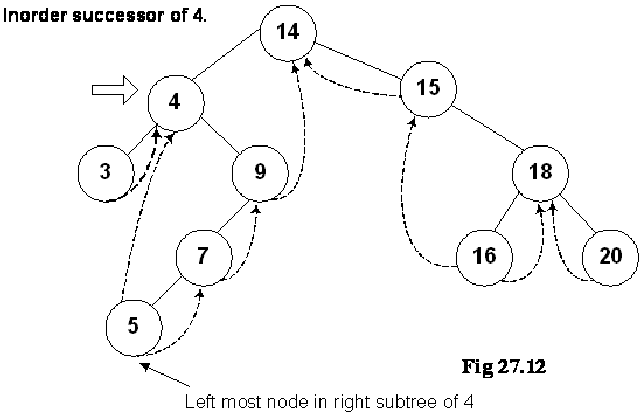
Where is Inorder Successor?

We are at node 4 and want to find its inorder successor. If you remember the delete operation discussed in the previous lecture, where we searched for the inorder successor and found it to be the left-most node in the right subtree of the node.

In this figure, the right subtree of 4 is starting from node 9 and ending at node 5. Node 5 is the left most node of it and this is also the inorder successor of node 4. We cannot go to node 5 directly from node 4, we go to node 9 first then node 7 and finally to node 5.

We move from node 9 to node 5 following the normal tree link and not thread. As long as the normal left tree link is there of a node, we have set the LTH flag to child. When we reach at node 5, the left link is a thread and it is indicated with a flag. See the while loop given in the above routine again:

while(p->LTH == child)

p = p->L;

return p;

Inorder Traversal

Now by using this routine, we try to make our inorder traversal procedure that is non-recursive and totally stack free.

If we can get things started correctly, we can simply call nextInorder repeatedly (in a simple loop) and move rapidly around the tree inorder printing node labels (say) - without a stack.

The pointer p is pointing to the root node of the tree. If we start traversing from this node and pass this root node pointer to our routine nexInorder above, it will create a problem.

We see the routine again to see the problem area clearly:

TreeNode* nextInorder(TreeNode* p)

{

if(p->RTH == thread)

return(p->R);

else {

p = p->R;

while(p->LTH == child)

p = p->L;

return p;

}

}

In the first part, it is checking for the RTH flag to be set to thread, which is not the case for the root node. The control will be passed to the else part of the routine. In else part, in the very first step, we are moving towards right of root that is to node 15.

If we call nextInorder with the root of the binary tree, we're going to have some difficulty. The code won't work at all the way we want.

Note that in this tree inorder traversal, the first number we should print is 3 but now we have reached to node 15 and we don’t know how can we reach node 3. This has created a problem. In the lecture, we will make a small change in this routine to cater to this situation i.e. when a root node pointer is passed to it as a parameter. After that change the routine will work properly in case of root node also and it will be non-recursive, stack free routine to traverse the tree.

Inorder traversal in threaded trees

We have introduced the threads in the tree and have written the nextInorder routine. It is sure that the provision of the root can help this routine perform the inorder routine properly. It will go to the left most node before following the threads to find the inorder successors. The code of the routine is given below:

/* The inorder routine for threaded binary tree */ TreeNode* nextInorder(TreeNode* p){ if(p->RTH == thread) return(p->R); else { p = p->R; while(p->LTH == child) p = p->L; return p; } }

When we apply this routine on the sample tree, it does not work properly because the pointer that points to the node goes in the wrong direction. How can we fix this problem? Let’s review the threaded binary tree again:

In the above figure, we have a binary search tree. Threads are also seen in it. These threads points to the successor and predecessor.

Our nextInoder routine, first of all checks that the right pointer of the node is thread. It means that it does not point to any tree node. In this case, we will return the right pointer of the node as it is pointing to the inorder successor of that node. Otherwise, we will go to some other part. Here we will change the value of pointer p to its right before running a while loops as long as the left pointer is the node. That means the left child is not a thread. We move to the left of the pointer p and keep on doing so till the time the left pointer becomes a thread.

We will pass the root of the tree to the nextInorder routine. The pointer p is pointing to the node 14 i.e. the root node. As the right pointer of the node 14 is not a thread, so the pointer p will move to the node 15 as shown below:

Here we want the inorder traversal. It is obvious from the above figure that 15 is not the first value. The first value should be 3. This means that we have moved in the wrong direction. How this problem can be overcome? We may want to implement some logic that in case of the root node, it is better not to go towards the right side. Rather, the left side movement will be appropriate. If this is not the root node, do as usual. It may lend complexities to our code. Is there any other way to fix it? Here we will use a programming trick to fix it.

We will make this routine as a private member function of the class so other classes do not have access to it. Now what is the trick? We will insert a new node in the tree. With the help of this node, it will be easy to find out whether we are on the root node or not. This way, the pointer p will move in the correct direction.

Let’s see this trick. We will insert an extra node in the binary tree and call it as a dummy node. This is well reflected in the diagram of the tree with the dummy node. We will see where that dummy node has been inserted.

This dummy node has either no value or some dummy value. The left pointer of this node is pointing to the root node of the tree while the right pointer is seen pointing itself i.e. to dummy node. There is no problem in doing all these things. We have put the address of dummy node in its right pointer and pointed the left thread of the left most node towards the dummy node. Similarly the right thread of the right-most node is pointing to the dummy node. Now we have some extra pointers whose help will make the nextInorder routine function properly.

Following is a routine fastInorder that can be in the public interface of the class.

/* This routine will traverse the binary search tree */ void fastInorder(TreeNode* p) { while((p=nexInorder(p)) != dummy) cout << p->getInfo(); }

This routine takes a TreeNode as an argument that make it pass through the root of the tree. In the while loop, we are calling the nextInorder routine and pass it p. The pointer returned from this routine is then assigned to p. This is a programming style of C. We are performing two tasks in a single statement i.e. we call the nextInorder by passing it p and the value returned by this routine is saved in p. Then we check that the value returned by the nextInorder routine that is now actually saved in p, is not a dummy node. Then we print the info of the node. This function is called as:

fastInorder(dummy);

We are not passing it the root of the tree but the dummy node. Now we will get the correct values and see in the diagrams below that p is now moving in the right direction. Let’s try to understand this with the help of diagrams.

First of all we call the nextInorder routine passing it the dummy node.

The pointer p is pointing to the dummy node. Now we will check whether the right pointer of this node is not thread. If so, then it is advisable to move the pointer towards the right pointer of the node. Now we will go to the while loop and start moving on the left of the node till the time we get a node with the left pointer as thread. The pointer p will move from dummy to node 14. As the left pointer of node 14 is not thread so p will move to node 4. Again the p will move to node 3. As the left pointer of p is thread, the while loop will finish here. This value will be returned that is pointing to node 3. The node 3 should be printed first of all regarding the inorder traversal. So with the help of our trick, we get the right information.

Now the while loop in the fastInorder will again call the nextInorder routine. We have updated the value of p in the fastInorder that is now pointing to the node 3. This is shown in the figure below:

According to the code, we have to follow the right thread of the node 3 that is pointing to the node 4. Therefore p is now pointing to the node 4. Here 4 is inorder successor of 3. So the pointer p has moved to the correct node for inorder traversal.

As the right pointer of the node 4 is a link, p will move to node 9. Later, we will go on the left of nodes and reach at the node 5. Looking at the tree, we know that the inorder successor of the node 4 is node 5. In the next step, we will get the node 7 and so on. With the help of threads and links, we are successful in getting the correct inorder traversal. No recursive call has been made so far. Therefore stack is not used. This inorder traversal will be faster than the recursive inorder traversal. When other classes use this routine, it will be faster. We have not used any additional memory for this routine. We are using the null links and putting the values of thread in it. This routine is very simple to understand. In the recursive routines, we have to stop the recursion at some condition. Otherwise, it will keep on executing and lead to the aborting of our program.

Technorati Tags: ds tutorial,data structure tutorial,tree data structure,trees in data structure,tree ds,tree traversal data structure,tree types,types of trees,binary trees,binary search trees,bst,bst data structure,bst ds,complete binary search tree,non tree structure,linear tree,properties of trees,binary tree property