Huffman Encoding

There are other uses of binary trees. One of these is in the compression of data. This is known as Huffman Encoding. Data compression plays a significant role in computer networks. To transmit data to its destination faster, it is necessary to either increase the data rate of the transmission media or simply send less data. The data compression is used in computer networks. To make the computer networks faster, we have two options i.e. one is to somehow increase the data rate of transmission or somehow send the less data. But it does not mean that less information should be sent or transmitted. Information must be complete at any cost.

Suppose you want to send some data to some other computer. We usually compress the file (using winzip) before sending. The receiver of the file decompresses the data before making its use. The other way is to increase the bandwidth. We may want to use the fiber cables or replace the slow modem with a faster one to increase the network speed. This way, we try to change the media of transmission to make the network faster. Now changing the media is the field of electrical or communication engineers. Nowadays, fiber optics is used to increase the transmission rate of data.

With the help of compression utilities, we can compress up to 70% of the data. How can we compress our file without losing the information? Suppose our file is of size 1 Mb and after compression the size will be just 300Kb. If it takes ten minutes to transmit the 1 Mb data, the compressed file will take 3 minutes for its transmission. You have also used the gif images, jpeg images and mpeg movie files. All of these standards are used to compress the data to reduce their transmission time. Compression methods are used for text, images, voice and other types of data.

We will not cover all of these compression algorithms here. You will study about algorithms and compression in the course of algorithm. Here, we will discuss a special compression algorithm that uses binary tree for this purpose. This is very simple and efficient method. This is also used in jpg standard. We use modems to connect to the internet. The modems perform the live data compression. When data comes to the modem, it compresses it and sends to other modem. At different points, compression is automatically performed. Let’s discuss Huffman Encoding algorithm.

Huffman code is method for the compression of standard text documents. It makes use of a binary tree to develop codes of varying lengths for the letters used in the original message. Huffman code is also part of the JPEG image compression scheme. The algorithm was introduced by David Huffman in 1952 as part of a course assignment at MIT.

Now we will see how Huffman Encoding make use of the binary tree. We will take a simple example to understand it. The example is to encode the 33-character phrase:

"traversing threaded binary trees"

In the phrase we have four words including spaces. There is a new line character in the end. The total characters in the phrase are 33 including the space. We have to send this phrase to some other computer. You know that binary codes are used for alphabets and other language characters. For English alphabets, we use ASCII codes. It normally consists of eight bits. We can represent lower case alphabets, upper case alphabets, 0,1,…9 and special symbols like $, ! etc while using ASCII codes. Internally, it consists of eight bits. If you have eight bits, how many different patterns you can be have? You can have 256 different patterns. In English, you have 26 lower case and 26 upper case alphabets. If you have seen the ASCII table, there are some printable characters and some unprintable characters in it. There are some graphic characters also in the ASCII table.

In our example, we have 33 characters. Of these, 29 characters are alphabets, 3 spaces and one new line character. The ASCII code for space is 32 and ASCII code for new line character is 10. The ASCII value for ‘a’ is 95 and the value of A is 65. How many bits we need to send 33 characters? As every character is of 8 bits, therefore for 33 characters, we need 33 * 8 = 264. But the use of Huffman algorithm can help send the same message with only 116 bits. So we can save around 40% using the Huffman algorithm.

Let’s discuss how the Huffman algorithm works. The algorithm is as:

• List all the letters used, including the "space" character, along with the frequency with which they occur in the message.
• Consider each of these (character, frequency) pairs to be nodes; they are actually leaf nodes, as we will see.
• Pick the two nodes with the lowest frequency. If there is a tie, pick randomly amongst those with equal frequencies.
• Make a new node out of these two, and turn two nodes into its children.
• This new node is assigned the sum of the frequencies of its children.
• Continue the process of combining the two nodes of lowest frequency till the time only one node, the root is left.

Let’s apply this algorithm on our sample phrase. In the table below, we have all the characters used in the phrase and their frequencies.

Original text: traversing threaded binary trees size: 33 characters (space and newline) Letters : Frequency NL : 1 SP : 3 a : 3 b : 1 d : 2 e : 5 g : 1 h : 1

The new line occurs only once and is represented in the above table as NL. Then white space occurs three times. We counted the alphabets that occur in different words. The letter a occurs three times, letter b occurs just once and so on.

Now we will make tree with these alphabets and their frequencies.

We have created nodes of all the characters and written their frequencies along with the nodes. The letters with less frequency are written little below. We are doing this for the sake of understandings and need not to do this in the programming. Now we will make binary tree with these nodes. We have combined letter v and letter y nodes with a parent node. The frequency of the parent node is 2. This frequency is calculated by the addition of the frequencies of both the children.

In the next step, we will combine the nodes g and h. Then the nodes NL and b are combined. Then the nodes d and i are combined and the frequency of their parent is the combined frequency of d and i i.e. 4. Later, n and s are combined with a parent node. Then we combine nodes a and t and the frequency of their parent is 6. We continue with the combining of the subtree with nodes v and y to the node SP. This way, different nodes are combined together and their combined frequency becomes the frequency of their parent. With the help of this, subtrees are getting connected to each other. Finally, we get a tree with a root node of frequency 33.

We get a binary tree with character nodes. There are different numbers with these nodes that represent the frequency of the character. So far, we have learnt how to make a tree with the letters and their frequency

Huffman encoding is used in data compression. Compression technique is employed while transferring the data. Suppose there is a word-document (text file) that we want to send on the network. If the file is, say, of one MB, there will be a lot of time required to send this file. However, in case of reduction of size by half through compression, the network transmission time also get halved. After this example, it will be quite easy to understand the Hoffman encoding to compress a text file.

We know that Huffman code is a method for the compression of standard text documents. It makes use of a binary tree to develop codes of varying lengths for the letters used in the original message. Huffman code is also a part of the JPEG image compression scheme. David Huffman introduced this algorithm in the year 1952 as part of a course assignment at MIT.

In the previous lecture, we had started discussing a simple example to understand Huffman encoding. In that example, we were encoding the 32-character phrase: "traversing threaded binary trees". If this phrase were sent as a message in a network using standard 8-bit ASCII codes, we would have to send 8*32= 256 bits. However, the Huffman algorithm can help cut down the size of the message to 116 bits.

In the Huffman encoding, following steps are involved:

1. List all the letters used, including the "space" character, along with the frequency with which they occur in the message.
2. Consider each of these (character, frequency) pairs as nodes; these are actually leaf nodes, as we will see later.
3. Pick two nodes with the lowest frequency. If there is a tie, pick randomly amongst those with equal frequencies
4. Make a new node out of these two and develop two nodes as its children.
5. This new node is assigned the sum of the frequencies of its children.
6. Continue the process of combining the two nodes of lowest frequency till the time, only one node, the root, is left.

In the first step, we make a list of all letters (characters) including space and end line character and find out the number of occurrences of each letter/character. For example we ascertain how many times the letter ‘a’ is found in the file and how many times ‘b’ occurs and so on. Thus we find the number of occurrences (i.e. frequency) of each letter in the text file.

In the step 2, we consider the pair (i.e. letter and its frequency) as a node. We will consider these as leaf nodes. Afterwards, we pick two nodes with the lowest frequency in the list. If there are more than one pairs of same frequency, we will choose a pair randomly amongst those with equal frequencies.

Suppose, in a file, the letter ‘a’ occurs 50 times and ‘b’ and ‘c’ five times each. Here, ‘b’ and ‘c’ have the lowest frequency. We will take these two letters as leaf nodes and build the tree from these ones. As fourth step states, we make a new node as the parent of these two nodes. The ‘b’ and ‘c’ are its children. In the fifth step, we assign to this new node the frequency equal to the sum of the frequencies of its children. Thus a three-node tree comes into existence. This is shown in the following figure.

We continue this process of combining the two nodes of lowest frequency till the time, only one node i.e. the root is left.

Now we come back to our example. In this example, there is a text string as written below.

traversing threaded binary trees

The size of this character string is 33 (it includes 3 space characters and one new line character). In the first step, we perform the counting of different characters in the string manually. We do not assign a fake or zero frequency to a letter that is not present in the string. A programmer may be concerned only with the characters/letters that are present in the text. We see that the letters and their frequencies in the above text is as given below.

Character	frequency	character	frequency
NL	1	I	2
SP	3	n	2
A	3	r	5
B	1	s	2
D	2	t	3
E	5	v	3
G	1	y	1
H	1

Table 1: Frequency table

In the second step, we make nodes of these pairs of letters and frequencies. The following figure (fig 26.2) depicts the letters as nodes. We have written the frequency of each letter with the node. The nodes have been categorized with respect to the frequencies for simplicity. We are going to build the tree from downside i.e. from the lowest frequency.

Now according to third step, two nodes of lowest frequency are picked up. We see that nodes NL, b, g, h, v and y have the frequency 1. We randomly choose the nodes v and y. now, as the fourth step, we make a new node and join the leaf nodes v and y to it as its children. We assign the frequency to this new (parent) node equal to the sum of the frequencies of its children i.e. v and y. Thus in the fifth step; the frequency of this new node is 2. We have written no letter in this node as shown in the figure below.

2 is equal to sum of the frequencies of the two children nodes.

Now we continue this process with other nodes. Now we join the nodes g and h as children of a new node. The frequency of this node is 2 i.e. the sum of frequencies of g and h. After this, we join the nodes NL and b. This also makes a new node of frequency 2. Thus the nodes having frequency 1 have joined to the respective parent nodes. This process is shown in the following figure (Fig 26.3).

Now we come to the nodes with a frequency 2. Here we join the pair of nodes d and i and also the pair n and s. Resultantly, the two nodes coming into being after joining have the frequency 4. This frequency is the sum of the frequencies of their children. Now, we will bring the nodes, a and t together. The parent node of a and t has the frequency 6 i.e. the sum of a and t. These new nodes are shown in the following figure.

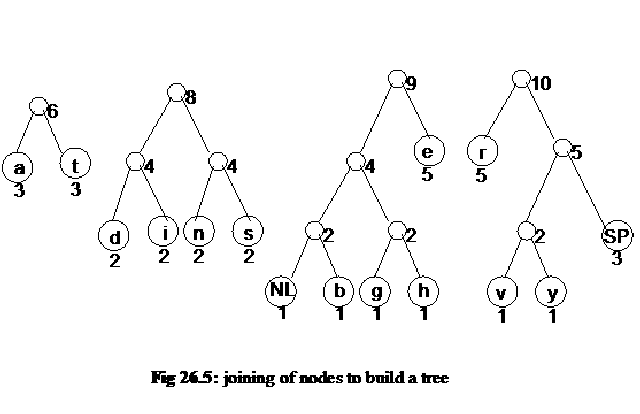
Now we consider these new nodes as inner nodes and build the tree upward towards the root. Now we take the node SP and join it with the node that is the parent of v and y. The resultant node has frequency 5 as the frequencies of its children are 2 and 5 respectively. Now we join these nodes of higher frequencies. In other words, the node r is joined with the newly created node of frequency 5 that is on the left side of node r in the figure 26.5. Thus a new node of frequency 10 is created. We join the node e and the node of frequency 4 on its right side. Resultantly, a new node of frequency 9 comes into existence. Then we join the nodes having frequency 4 and create a new node of frequency 8. The following figure shows the nodes created so far.

Now we will join the nodes of frequency 6 and 8 to create the node of frequency 14 and join the nodes of frequency of 9 and 10 to develop a new node of frequency of 19. At the end, we make the root node with the frequency 33 and it comprises nodes of frequency 14 and 19. Thus the tree is completed and shown in the following figure.

Now we will perform other steps of Hoffman encoding and develop character-encoding scheme needed for data compression.

To go ahead, we have to do the following steps.

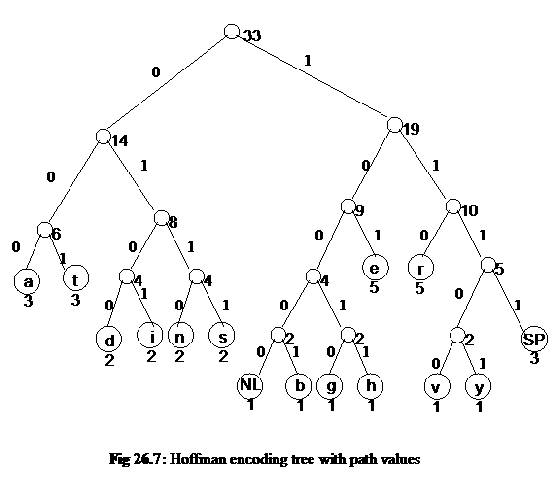
• Start at the root. Assign 0 to left branch and 1 to the right branch.
• Repeat the process down the left and right subtrees.
• To get the code for a character, traverse the tree from the root to the character leaf node and read off the 0 and 1 along the path.

We start from the root node of the tree and assign the value 0 to the left branch and 1 to the right branch. Afterwards, we repeat this value assigning at nodes in left and right subtrees. Thus all the paths have a value 0 or 1 as shown in the following figure. We will develop the code with the help of these path values.

In the last step, we get the code for the characters. To get the code for a character, there is need of traversing the tree from the root to the character leaf node and read off the 0 and 1 along the path. We start from the root and go to the letter of leaf node following the edges. 0 and 1 are written down in the order in which they come in this traversal to leaf node. For example, we want the code of letter d. To reach d from the root; we have to go through the nodes of frequency 14. This path has value 0. Here, 0 will be the first digit in the code of d. From 14, we go to node of frequency 8. This link (from 14 to 8) has value 1. Thus the second digit in code is 1. From node of frequency 8, we go to node of frequency 4 to its left side. This side has value 0, meaning that 0 is the third digit of code. From 4, we finally go to d and in this link we get the value 0. Thus we see that to reach at d from the root, we have gone through the branches 0, 1, 0 and 0. Thus, the code of letter d is 0100. Similarly the code of i is 0101. The same way, we find the code for each letter in the tree. The following table shows the letters and their correspondent codes.

character	code	character	code
NL	10000	i	0101
SP	1111	n	0110
a	000	r	110
b	10001	s	0111
d	0100	t	001
e	101	v	11100
g	10010	y	11101
h	10011

Table 2: Hoffman code table

We know that every character is stored in the computer in binary format. Each character has a code, called ASCII code. The ASCII code of a character consists of ones and zeros i.e. it is in binary form. ASCII code is of eight bits. Normally, we remember the decimal value of the characters. For example, letter ‘A’ has decimal value 65. We can easily convert the decimal value into binary one in bit pattern. We need not to remember these values. ASCII value of any character can be found from the ASCII table. The ASCII code of each character is represented in eight bits with different bit patterns.

Here in the example, we assign a code of our own (i.e. Hoffman code) to the letters that are in the message text. This code also consists of ones and zeros. The above table shows the characters and their Hoffman code. Now we come back to the message text from which we developed the tree and assigned codes to the letters in the text.

Look at the table (Table 2) shown above. Here we notice that the code of letters is of variable length. We see that letters with higher frequency have shorter code. There are some codes with a length five that are the codes of NL, b, g, h, v and y. Similarly we see that the letters SP, d, i, n and s have codes of length four. The codes of the remaining letters have length three. If we look at the frequency table (Table 1) of these letters, we see that the letters with some higher frequency like a, e, r, and t, have the code of shorter length, whereas the letters of lower frequency (like NL, b, g, h, v and y) have codes of larger length.

We see in the table of the Hoffman codes of the letters that there will be need of 5, 4 or in some codes only 3 bits to represent a character, whereas in ASCII code, we need 8 bits for each character. Now we replace the letters in the text message with these codes. In the code format i.e. in the form of ones and zeros, the message becomes as under.

Our original message was

traversing threaded binary trees

The encoded form of the message is as under

t r a v e r s i n g t 00111000011100101110011101010110100101111001 100111101010000100101010011111000101010110000 110111011111001110101101011110000

We see that there are only ones and zeros in the code of message. Some letters have been shown with their corresponding code. The first three bits 001 are for letter ‘t’. The next three bits 110 are for letter ‘r’. After this the letter ‘a’ has three bits i.e. 000. Next to it is the letter ‘v’ that has five bits. These bits are 11100 (shaded in the figure). Similarly we have replaced all the letters of the message with their corresponding Hoffman code. The encoded message is shown above.

Let’s compare this Hoffman encoded message with the encoding of message with ASCII code. The ASCII code encoding means that if we have encoded this message with 8 bits per character, the total length of message would be 264. As there are 33 characters, so the total length is 33 x 8 = 264. But in the Hoffman encoded message (written in above table), there are only 120 bits. This number of bits is 54% less than the number of bits in ASCII encoding form. Thus we can send the message with almost half of the original length to a receiver.

Here the Hoffman encoding process comes to an end. In this process, we took a message, did the frequency count of its characters and built a tree from these frequencies. From this tree, we made codes of letters consisting of ones and zeros only. Then with the help of these codes, we did the data compression. In this process we saw that less data is required for the same message.

Now an important thing to be noted is regarding the tree building. We have built the tree with our choices of nodes with same and different frequencies. Now if we have chosen the nodes to join in different way, the tree built would be in a different form. This results in the different Hoffman code for the letters. These will be in ones and zeros but with different pattern. Thus the encoded message would have different codes for the letters. Now the question arises how does the receiver come to know that what code is used for what letter? The answer is very simple that the sender has to tell the receiver that he is using such codes for letters. One way to tackle this problem is that the sender sends the tree built through the use of frequencies, to the receiver to decode the message. The receiver keeps a copy of this tree. Afterwards, when the sender sends a message, the receiver will match it with respect to bit pattern with the tree to see that what letter the sender has sent. The receiver will find the letter for the first 2, 3, 4 or what numbers of bits match to a letter that it has in the tree as the receiver also has a copy of the tree. We know that a tree has a root, inner nodes and leaf node(s). The leaf node is a node whose left and right links is NULL. An inner node has a left or right or both children. Now consider that the receiver has the same tree data structure that the sender used to construct the codes. The sender has sent the message that we have discussed above. The sender sends the 122 bits encoded message to the receiver. The receiver will take the first bit of message and being on the root of the tree, it will decide that on what side this bit will go. If the bit is zero, it will go to the left of the root. However, if the bit is one, it will go to the right side of the root before reaching to the child node. The next bit will go to the next level of the tree to the left or right side depending on zero or one. Thus the traversal will go one level down on receiving a bit. If we (the receiver) are on a path of the tree where the leaf node is at level 6, it cannot reach the leaf node unless the receiver receives 6 bits. We consider the case of letter ‘e’ whose code was of three bits. In this case, we go to the first level by first bit and the second bit takes us to the third level. Finally on reaching the third level with the third bit, we get the leaf node. We know that this node is letter ‘e’ as the sender has sent us (as receiver) the whole tree with the characters in the nodes. Thus after traversing the three bits, the receiver has confirmed that it has received the letter ‘e’. Now on receiving the fourth bit, the receiver will go back to the root and continue to choose the path i.e. on zero it will go to the left and on one it will go to right. This way, it will reach the leaf node. The character at that node will be the next character of the message. The bit pattern that was comprised of following these links in the tree is extracted from the message. On the next bit, the receiver again goes to the root node and the previous procedure is repeated to find the next character. This way, it decodes the whole message.

The compression is very useful technique especially for communication purposes. Suppose that we have to send a file of one Mb. Here each line in the file can be compressed to 50 or 60 percent. Thus the file of one MB will be compressed to half MB and can be sent more easily.

There is one more thing about this tree. When we started to build the tree from leaf nodes i.e. bottom-up build of tree, we saw that there were choices for us to choose any two leaf nodes to join. In our example, we chose them at random. The other way to do it is the priority queue. We have seen the example of bank simulation. There we used a priority queue for the events. We know that in a priority queue, the elements do not follow the FIFO (first in first out) rule. But the elements have their position in the queue with respect to a priority. In the example of bank simulation, in the Event Queue, we remove the element from the queue that was going to occur first in the future. We can use priority queue here in such a way that we put the letters in the queue with respect to their frequencies. We will put and remove letters from the queue with respect to their frequency. In this priority queue, the character with lowest frequency is at the start of the queue. If two characters have the same frequency, these will be one after the other in the queue. The character with the larger frequency will be in the last of the queue. Now we take two frequencies from the queue and join them to make a new node. Suppose that the nodes that we joined have frequency 1 and 2 respectively. So the frequency of the new node will be 3. We put this new node in the queue. It takes its position in the queue with respect to its frequency as we are using the priority queue. It is evident in procedure that we proceed to take two nodes form the queue. These are removed and their parent node goes back to the queue with a new frequency. This procedure goes on till the time the queue is empty. The last node that becomes in the queue in the result of this procedure is the root node. This root node has frequency 33 if we apply this procedure to our previous example.

Let’s talk about some general things related to Hoffman encoding. We use modems to connect to Internet. These modems do the compression. The modem has a compression feature. The modem has a chip that performs the task of compression. When we give a sentence of say 80 characters to the modem to send, the modem makes a Hoffman encoded tree of these characters. Then it will make codes from this tree. We know that there is also a modem on the other end that will decode this message. The sender modem will send the tree structure to the receiver. Now the sender modem will send the data in compressed form. The receiving modem will decode this compressed data by using the Hoffman encoded tree. Now the question arises, will these codes be useful for other messages? In our example message the letter ‘y’ has lower frequency and code of five bits. It may happen that in some messages ‘y’ has higher frequency, needing code of less number of bits. To solve this problem, the modems (sender and receiver) revise the codes after a certain time period or after a particular number of bytes. In this revision, they build a new Hoffman tree and exchange it to use it for communication for the next time period or for the next fixed number of bytes.

There is some other compression techniques/algorithms for compression. The zip routines like winzip and the jpeg, mpeg and other image formatting routines use different algorithms for compression. We will read the compression algorithm in detail in the course of Algorithms.

Technorati Tags: huffman encoding,huffman encoding tutorial,huffman encoding data structure,ds tutorial,data structure tutorial,tree data structure,trees in data structure,tree ds,tree traversal data structure,tree types,types of trees,binary trees,binary search trees,bst,bst data structure,bst ds,complete binary search tree,non tree structure,linear tree