Deleting a Node From Binary Search Tree

 

Until now, we have been discussing about adding data elements in a binary tree but we may also require to delete some data (nodes) from a binary tree. Consider the case where we used binary tree to implement the telephone directory, when a person leaves a city, its telephone number from the directory is deleted.

It is common with many data structures that the hardest operation is deletion. Once we have found the node to be deleted, we need to consider several possibilities.

For case 1, If the node is a leaf, it can be deleted quite easily.

See the tree figure below.

Suppose we want to delete the node containing number 3, as it is a leaf node, it is pretty straight forward. We delete the leaf node containing value 3 and point the right subtree pointer to NULL.

For case 2, if the node has one child, the node can be deleted after its parent adjusts a pointer to bypass the node and connect to inorder successor.

If we want to delete the node containing number 4 then we have to adjust the right subtree pointer in the node containing value 2 to the inorder successor of 4. The important point is that the inorder traversal order has to be maintained after the delete.

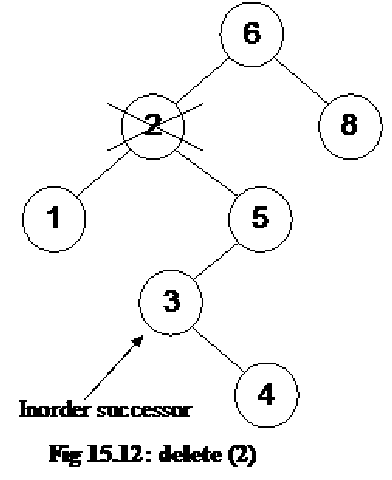
The case 3 is bit complicated, when the node to be deleted has both left and right subtrees.

The strategy is to replace the data of this node containing the smallest data of the right subtree and recursively delete that node.

Let’s see this strategy in action. See the tree below:

In this tree, we want to delete the node containing number 2. Let’s do inorder traversal of this tree first. The inorder traversal give us the numbers: 1, 2, 3, 4, 5, 6 and 8.

In order to delete the node containing number 2, firstly we will see its right subtree and find the left most node of it.

The left most node in the right subtree is the node containing number 3. Pay attention to the nodes of the tree where these numbers are present. You will notice that node containing number 3 is not right child node of the node containing number 2 instead it is left child node of the right child node of number 2. Also the left child pointer of node containing number 3 is NULL.

After we have found the left most node in the right subtree of the node containing number 2, we copy the contents of this left most node i.e. 3 to the node to be deleted with number 2.

Next step is to delete the left most node containing value 3. Now being the left most node, there will be no left subtree of it, it might have a right subtree. Therefore, the deletion of this node is the case 2 deletion and the delete operation can be called recursively to delete the node.

Now if we traverse the tree in inorder, we get the numbers as: 1, 3, 4, 5, 6 and 8. Notice that these numbers are still sorted.

Technorati Tags: ds tutorial,data structure tutorial,tree data structure,trees in data structure,tree ds,tree traversal data structure,tree types,types of trees,binary trees,binary search trees,bst,bst data structure,bst ds,complete binary search tree,non tree structure,linear tree,binary search tree,deleting a node from bst,deleting node binary search tree