A queue is a linear data structure into which items can only be inserted at one end and removed from the other. In contrast to the stack, which is a LIFO (Last In First Out) structure, a queue is a FIFO (First In First Out) structure.
The usage of queue in daily life is pretty common. For example, we queue up while depositing a utility bill or purchasing a ticket. The objective of that queue is to serve persons in their arrival order; the first coming person is served first. The person, who comes first, stands at the start followed by the person coming after him and so on. At the serving side, the person who has joined the queue first is served first. If the requirement is to serve the people in some sort of priority order, there is a separate data structure that supports priorities. The normal queue data structure, presently under discussion, only supports FIFO behavior.
Now, let’s see what are the operations supported by the queue.
Queue Operations
The queue data structure supports the following operations:
| Operation | Description |
| enqueue(X) | Place X at the rear of the queue. |
| dequeue() | Remove the front element and return it. |
| front() | Return front element without removing it. |
| isEmpty() | Return TRUE if queue is empty, FALSE otherwise |
Implementing Queue
There are certain points related to the implementation of the queue. Suppose we are implementing queue with the help of the linked -list structure. Following are the key points associated with the linked list implementations:
- Insert works in constant time for either end of a linked list.
- Remove works in constant time only.
- Seems best that head of the linked list be the front of the queue so that all removes will be from the front.
- Inserts will be at the end of the list.
The above figure shows queue elements on the left with two pointers front and rear. This is an abstract view of the queue, independent of its implementation method of array or linked list. On the right side is the same queue ,using linked list and pointers of front and rear. When dequeue() function is called once, the front element 1 is removed. The picture of the queue showing one element removal is also depicted below. Note that front pointer has been moved to the next element 7 in the list afer removing the front element 1.
Now at this stage of the queue, we will call enqueue (9) to insert an element 9 in it. . The following figure shows that the new element is inserted at the rear end and rear pointer starts pointing this new node with element 9.
At this point of time, the code of these functions of dequeue() and enqueue() should not be an issue.
Note that in this queue data structure, the new elements are inserted at rear end and removed from the front. This is in contrast to stack structure where the elements are inserted and removed from the same end.
Let’s see the code for queue operations:
| /* Remove element from the front */ 1. int dequeue() 2. { 3. int x = front->get(); 4. Node* p = front; 5. front = front->getNext(); 6. delete p; 7. return x; 8. } /* Insert an element in the rear */ 9. void enqueue(int x) 10. { 11. Node* newNode = new Node(); 12. newNode->set(x); 13. newNode->setNext(NULL); 14. rear->setNext(newNode); 15. rear = newNode; 16. } |
In dequeue() operation, at line 3, the front element is retrieved from the queue and assigned to the int variable x.
In line 4, the front pointer is saved in Node pointer variable p.
In line 5, the front pointer is moved forward by retrieving the address of the next node by using front->getNext() and assigning it to the front pointer.
In line 6, the node pointed to by the front pointer is deleted by using delete front statement.
At the end of dequeue() implementation, the value of deleted node that was saved in the int variable x, is returned back.
The enqueue(int ) is used to add an element in the queue. It inserts the element in the rear of the queue. At line 11, a new Node object is created using the new Node() statement and the returned starting address of the created object is assigned to the newNode pointer variable.
In line 12, the value of the passed in parameter x, is set in the newly created node object using the set() method.
In line 13, the next pointer in the newly created node is set to NULL.
In line 14, the newly created node is set as the next node of the node currently pointed by the rear pointer.
Ine line 15, the rear pointer is set to point to the newly created node.
The code of two smaller functions is as under:
| /* To retrieve the front element */ int front() { return front->get(); } /* To check if the queue is empty */ int isEmpty() { return ( front == NULL ); } |
The front() method is used to retrieve the front element. This is the oldest element inserted in the queue. It uses the get() method of the Node class.
The isEmpty() method is used to check whether the queue is empty or not. It checks the address inside the front pointer, if it is NULL. It will return true indicating that the queue is empty or vice versa.
While studying stack data structure, we implemented it by using both array and linked list. For queue, until now we have been discussing about implementing queue using linked list. Now, let’s discuss implementing queue with the help of an array.
Queue using Array
A programmer keeps few important considerations into view account before implementing a queue with the help of an array:
If we use an array to hold the queue elements, both insertions and removal at the front (start) of the array are expensive. This is due to the fact that we may have to shift up to “n” elements.
For the stack, we needed only one end but for a queue, both are required. To get around this, we will not shift upon removal of an element.
In the above figure, queue implementation using array is shown. As the array size is 8, therefore, the index of the array will be from 0 to 7. The number of elements inside array are 1, 7, 5 and 2, placed at start of the array. The front and rear in this implementation are not pointers but just indexes of arrays. front contains the starting index i.e. 0 while rear comprises 3.
Let’s see, how the enqueue() works:
As shown in the above diagram, an element i.e. 6 has been inserted in the queue. Now, the rear index is containing 4 while the front has the same 0 index. Let’s see the figure of the array when another element 8 is inserted in the queue.
When an element is removed from the queue. It is removed from the front index.
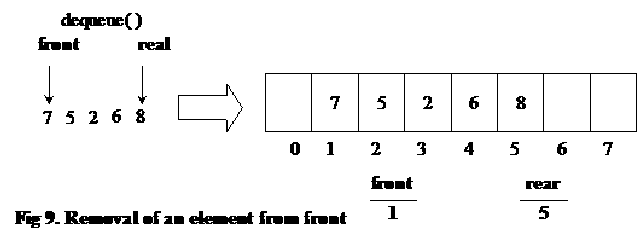
After another call of dequeue() function:
With the removal of element from the queue, we are not shifting the array elements. The shifting of elements might be an expensive exercise to perform and the cost is increased with the increase in number of elements in the array. Therefore, we will leave them as it is.
After insertion of two elements in the queue, the array that was used to implement it, has reached its limit as the last location of the array is in use now. We know that there is some problem with the array after it attained the size limit. We observed the similar problem while implementing a stack with the help of an array.
We can also see that two locations at the start of the array are vacant. Therefore, we should can consider how to use those locations appropriately in to insert more elements in the array.
Although, we have insert and removal operations running in constantly, yet we created a new problem that we cannot insert new elements even though there are two places available at the start of the array. The solution to this problem lies in allowing the queue to wrap around.
How can we wrap around? We can use circular array to implement the queue. We know how to make a linked list circular using pointers. Now we will see how can we make a circular array.
The number of locations in the above circular array are also eight, starting from index 0 to index 7. The index numbers are written outside the circle incremented in the clock-wise direction. To insert an element 21 in the array , we insert this element in the location, which is next to index 7.
Now, we will have to maintain four variables. front has the same index 2 while the, size is 8. ‘ rear’ has moved to index 0 and noElements is 7. Now, we can see that rear index has decreased instread of increasing. It has moved from index 7 to 0. front is containing index 2 i.e. higher than the index in rear. Let’ see, how do we implement the enqueue() method.
| void enqueue( int x) { 1. rear = (rear + 1) % size; 2. array[rear] = x; 3. noElements = noElements + 1; } |
In line 1 of the code, 1 is added in rear and the mod operator (that results in remainder of the two operands) is applied with size variable. This expression on the right of assignment in line 1 can result from 0 to 7 as size is containing value 8. This operator ensures that value of this expression will always be from 0 to 7 and increase or decrease from this. This resultant is assigned to the rear variable.
In line 2, the x (the value passed to enqueue() method to insert in the queue) is inserted in the array at the rear index position. Therefore, in the above case, the new element 21 is inserted at index 0 in the array.
In line 3, noElements is added to accumulate another element in the queue.
Let’s add another element in the queue.
Now, the queue, rather the array has become full. It is important to understand, that queue does not have such characteristic to become full. Only its implementation array has become full. To resolve this problem, we can use linked list to implement a queue. For the moment, while working with array, we will write the method isFull(), to determine the fullness of the array.
| int isFull() { return noElements == size; } int isEmpty() { return noElements == 0; } |
isFull() returns true if the number of elements (noElements) in the array is equal to the size of the array. Otherwise, it returns false. It is the responsibility of the caller of the queue structure to call isFull() function to confirm that there is some space left in the queue to enqueue() more elements.
Similarly isEmpty() looks at the number of elements (noElements) in the queue. If there is no element, it returns true or vice versa..
Let’s see the dequeue() method.
| int dequeue() { int x = array[front]; front = (front + 1) % size; noElements = noElements - 1; return x; } |
In the first line, we take out an element from the array at front index position and store it in a variable x. In the second line, front is incremented by 1 but as the array is circular, the index is looped from 0 to 7. That is why the mod (%) is being used. In the third line, number of elements (noElements) is reduced by 1 and finally the saved array element is returned.















No comments:
Post a Comment