We have earlier discussed the properties of the binary trees besides talking about the internal and external nodes’ theorem. Now we will discuss another property of binary trees that is related to its storage before dilating upon the complete binary tree and the heap abstract data type.
Here is the definition of a complete binary tree:
- A complete binary tree is a tree that is completely filled, with the possible exception of the bottom level.
- The bottom level is filled from left to right.
A binary tree T with n levels is complete if all levels except possibly the last are completely full,
and the last level has all its nodes to the left side.You may find the definition of complete binary tree in the books little bit different from this. A perfectly complete binary tree has all the leaf nodes. In the complete binary tree, all the nodes have left and right child nodes except the bottom level. At the bottom level, you will find the nodes from left to right. The bottom level may not be completely filled, depicting that the tree is not a perfectly complete one. Let’s see a complete binary tree in the figure below:
and the last level has all its nodes to the left side.You may find the definition of complete binary tree in the books little bit different from this. A perfectly complete binary tree has all the leaf nodes. In the complete binary tree, all the nodes have left and right child nodes except the bottom level. At the bottom level, you will find the nodes from left to right. The bottom level may not be completely filled, depicting that the tree is not a perfectly complete one. Let’s see a complete binary tree in the figure below:
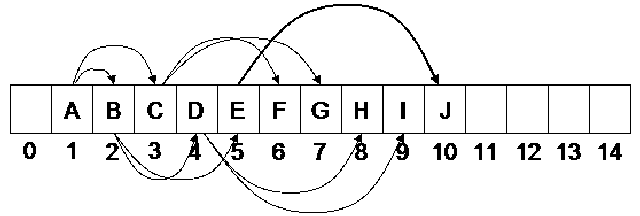
In the above tree, we have nodes as A, B, C, D, E, F, G, H, I, J. The node D has two children at the lowest level whereas node E has only left child at the lowest level that is J. The right child of the node E is missing. Similarly node F and G also lack child nodes. This is a complete binary tree according to the definition given above. At the lowest level, leaf nodes are present from left to right but all the inner nodes have both children. Let’s recap some of the properties of complete binary tree.
- A complete binary tree of height h has between 2h to 2h+1 –1 nodes.
- The height of such a tree is log2N where N is the number of nodes in the tree.
- Because the tree is so regular, it can be stored in an array. No pointers are necessary.
We have taken the floor of the log2 N. If the answer is not an integer, we will take the next smaller integer. So far, we have been using the pointers for the implementation of trees. The treeNode class has left and right pointers. We have pointers in the balance tree also. In the threaded trees, these pointers were used in a different way. But now we can say that an array can be stored in a complete binary tree without needing the help of any pointer.
Now we will try to remember the characteristics of the tree. 1) The data element can be numbers, strings, name or some other data type. The information is stored in the node. We may retrieve, change or delete it. 2) We link these nodes in a special way i.e. a node can have left or right subtree or both. Now we will see why the pointers are being used. We just started using these. If we have some other structure in which trees can be stored and information may be searched, then these may be used. There should be reason for choosing that structure or pointer for the manipulation of the trees. If we have a complete binary tree, it can be stored in an array easily.
The following example can help understand this process. Consider the above tree again.
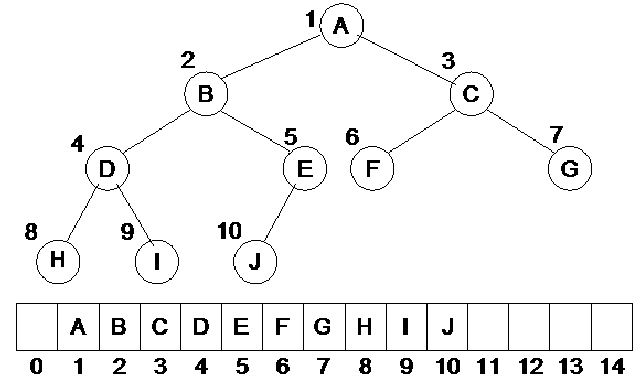
We have seen an array of size 15 in which the data elements A, B, C, D, E, F, G, H, I, J have been stored, starting from position 1. The question arises why we have stored the data element this way and what is justification of storing the element at the 1st position of the array instead of 0th position? You will get the answers of these very shortly.
The root node of this tree is A and the left and right children of A are B and C. Now look at the array. While storing elements in the array, we follow a rule given below:
- For any array element at position i, the left child is at 2i, the right child is at (2i +1) and the parent is at floor(i/2).
In the tree, we have links between the parent node and the children nodes. In case of having a node with left and right children, stored at position i in the array, the left child will be at position 2i and the right child will be at 2i+1 position. If the value of i is 2, the parent will be at position 2 and the left child will be at position 2i i.e. 4 .The right child will be at position 2i+1 i.e. 5. You must be aware that we have not started from the 0th position. It is simply due to the fact if the position is 0, 2i will also become 0. So we will start from the 1st position, ignoring the 0th.
Lets see this formula on the above array. We have A at the first position and it has two children B and C. According to the formula the B will be at the 2i i.e. 2nd position and C will be at 2i+1 i.e. 3rd position. Take the 2nd element i.e. B, it has two children D and E. The position of B is 2 i.e. the value of i is 2. Its left child D will be at positon 2i i.e. 4th position and its right child E will be at position 2i+1 i.e. 5. This is shown in the figure below:
If we want to keep the tree’s data in the array, the children of B should be at the position 4 and 5. This is true. We can apply this formula on the remaining nodes also. Now you have understood how to store tree’s data in an array. In one respect, we are using pointers here. These are not C++ pointers. In other words, we have implicit pointers in the array. These pointers are hidden. With the help of the formula, we can obtain the left and right children of the nodes i.e. if the node is at the ith position, its children will be at 2i and 2i+1 position. Let’s see the position of other nodes in the array.
As the node C is at position 3, its children should be at 2*3 i.e. 6th position and 2*3+1 i.e. 7th position. The children of C are F and G which should be at 6th and 7th position. Look at the node D. It is at position 4. Its children should be at position 8 and 9. E is at position 5 so its children should be at 10 and 11 positions. All the nodes have been stored in the array. As the node E does not have a right child, the position 11 is empty in the array.
You can see that there is only one array going out of E. There is a link between the parent node and the child node. In this array, we can find the children of a node with the help of the formula i.e. if the parent node is at ith position, its children will be at 2i and 2i+1 position. Similarly there is a link between the child and the parent. A child can get its parent with the help of formula i.e. if a node is at ith position, its parent will be at floor(i/2) position. Let’s check this fact in our sample tree. See the diagram below:
Consider the node J at position is 10. According to the formula, its parent should be at floor(10/2) i.e. 5 which is true. As the node I is at position 9, its parent should be at floor(9/2) i.e. 4. The result of 9/2 is 4.5. But due to the floor, we will round it down and the result will be 4. We can see that the parent of I is D which is at position 4. Similarly the parent of H will be at floor(8/2). It means that it will be at 4. Thus we see that D is its parent. The links shown in the figure depict that D has two children H and I. We can easily prove this formula for the other nodes.
From the above discussion we note three things. 1) We have a complete binary tree, which stores some information. It may or may not be a binary search tree. This tree can be stored in an array. We use 2i and 2i+1 indexing scheme to put the nodes in the array. Now we can apply the algorithms of tree structure on this array structure, if needed.
Now let’s talk about the usage of pointers and array. We have read that while implementing data structures, the use of array makes it easy and fast to add and remove data from arrays. In an array, we can directly locate a required position with the help of a single index, where we want to add or remove data. Array is so important that it is a part of the language. Whereas the data structures like tree, stack and queue are not the part of C or C++ language as a language construct. However we can write our classes for these data structures. As these data structures are not a part of the language, a programmer can not declare them directly. We can not declare a tree or a stack in a program. Whereas we can declare an array directly as int x []; The array data type is so efficient and is of so common use that most of the languages support it. The compiler of a language handles the array and the programmer has to do nothing for declaring and using an array.
We have built the binary trees with pointers. The use of pointers in the memory requires some time. In compilers or operating system course, we will read that when a program is stored in the memory and becomes a process, the executable code does not come in the memory. There is a term paging or virtual memory. When a program executes, some part of it comes in the memory. If we are using pointers to go to different parts of the program, some part of the code of program will be coming (loading) to memory while some other may be removed (unloading) from the memory. This loading and unloading of program code is executed by a mechanism, called paging. In Windows operating system, for this virtual memory (paging mechanism), a file is used, called page file. With the use of pointers, this process of paging may increase. Due to this, the program may execute slowly. In the course of Operating System and Compilers, you will read in detail that the usage of pointers can cause many problems.
So we should use arrays where ever it can fulfill our requirements. The array is a very fast and efficient data structure and is supported by the compiler. There are some situations where the use of pointers is beneficial. The balancing of AVL tree is an example in this regard. Here pointers are more efficient. If we are using array, there will be need of moving a large data here and there to balance the tree.
From the discussion on use of pointers and array, we conclude that the use of array should be made whenever it is required. Now it is clear that binary tree is an important data structure. Now we see that whether we can store it in an array or not. We can surely use the array. The functions of tree are possible with help of array. Now consider the previous example of binary tree. In this tree, the order of the nodes that we maintained was for the indexing purpose of the array. Moreover we know the level-order traversal of the tree. We used queue for the level-order of a tree. If we do level-order traversal of the tree, the order of nodes visited is shown with numbers in the following figure.
In the above figure, we see that the number of node A is 1. The node B is on number 2 and C is on number 3. At the next level, the number of nodes D, E, F and G are 4, 5, 6 and 7 respectively. At the lowest level, the numbers 8, 9 and 10 are written with nodes H, I and J respectively. This is the level-order traversal. You must remember that in the example where we did the preorder, inorder and post order traversal with recursion by using stack. We can do the level-order traversal by using a queue. Now after the level-order traversal, let’s look at the array shown in the lower portion of the above figure. In this array, we see that the numbers of A, B, C and other nodes are the same as in the level-order traversal. Thus, if we use the numbers of level-order traversal as index, the values are precisely stored at that numbers in the array. It is easy for us to store a given tree in an array. We simply traverse the tree by level-order and use the order number of nodes as index to store the values of nodes in the array. A programmer can do the level-order traversal with queue as we had carried out in an example before. We preserve the number of nodes in the queue before traversing the queue for nodes and putting the nodes in the array. We do not carry out this process, as it is unnecessarily long and very time consuming. However, we see that the level-order traversal directly gives us the index of the array depending upon which data can be stored.
Now the question arises if we can store the binary tree in an array, why there should be the use of pointers? It is very simple that an array is used when the tree is a complete binary tree. Array can also be used for the trees that are not complete binary trees. But there will be a problem in this case. The size of the array will be with respect to the deepest level of the tree according to the traversal order. Due to incomplete binary tree, there will be holes in the array that means that there will be some positions in the array with no value of data. We can understand it with a simple example. Look at the following figure where we store a complete binary tree in an array by using 2i and 2i+1 scheme. Here we stored the nodes from A to J in the array at index 1 to 10 respectively.
Suppose that this tree is not complete. In other words, B has no right subtree that means E and J are not there. Similarly we suppose that there is no right subtree of A. Now the tree will be in the form as shown in the following figure (29.2).
In this case, the effort to store this tree in the array will be of no use as the 2i and 2i+1 scheme cannot be applied to it. To store this tree, it may be supposed that there are nodes at the positions of C, F, G, E and J (that were there in previous figure). Thus we transform it into a complete binary tree. Now we store the tree in the array by using 2i and 2i +1 scheme. Afterwards, the data is removed from the array at the positions of the imaginary nodes (in this example, the nodes are C, F, G, E and J). Thus we notice that the nodes A, B and H etc are at the positions, depicting the presence of a complete binary tree. The locations of C, f, G, E and J in the array are empty as shown in the following figure.
Now imagine that an incomplete binary tree is very deep. We can store this tree in the array that needs to be of large size. There will be holes in the array. This is the wastage of memory. Due to this reason, it is thought that if a tree is not completely binary, it is not good to store it into an array. Rather, a programmer will prefer to use pointers for the storage.
Remember that two things are kept into view while constructing a data structure that is memory and time. There should such a data structure that could ensure the running of the programs in a fast manner. Secondly, a data structure should not use a lot of memory so that a large part of memory occupied by it does not go waste. To manage the memory in an efficient way, we use dynamic memory with the help of pointers. With the use of pointers only the required amount of memory is occupied.
We also use pointers for complex operations with data structure as witnessed in the deletion operation in AVL tree. One of the problems with arrays is that the memory becomes useless in case of too many empty positions in the array. We cannot free it and use in other programs as the memory of an array is contiguous. It is difficult to free the memory of locations from 50 to 100 in an array of 200 locations. To manage the memory in a better way, we have to use pointers.
Technorati Tags: ds tutorial,data structure tutorial,tree data structure,trees in data structure,tree ds,tree traversal data structure,tree types,types of trees,binary trees,binary search trees,bst,bst data structure,bst ds,complete binary search tree,non tree structure,linear tree,complete binary tree




![clip_image001[4] clip_image001[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhm-_xE-ED80KUpOqW7T02Rhoh17nD4TX3h6SLI1-DKVuU7GnozAFAGRQGBbKthfsuQzFnJKlxzLgdIjtG4WIf2NQwbgSgXHnx08JnjuhzBtqWghmQ4NsYjl8wPV1UKCFywskOfD1_y-G0/?imgmax=800)
![clip_image002[6] clip_image002[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjwEvpOrDgkqTlVEne1xMqSyfJ1oP_AVQZcLnBOdQnFKzD7BQUXmWK31_WGTqgsrXJmyqlt6VoxqgYyh84PGE4DfngnWFbINYF1b6-T4FP6l6eM_1t4HDDHisDG55iEXwBgIITlUm5DLEA/?imgmax=800)
![clip_image003[6] clip_image003[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjaoPE1ej1AjjJXPIlxRVd0dfJIh03BjKSFtKwkq4dV_3kLgZPl1sG-Lnr_Yu1-mVWRFZ3ovr9NYiMtfBFy8Zfo-BguFSYGpK9bITsn-ZBm2mq7KjuVjUjqg1YZEm280-F9CBMpZIaYCC4/?imgmax=800)



great explanation of concept and use of array or pointer for CBT.
ReplyDeleteThanks alot ! Great job...very helpful for me and my friends.
ReplyDeleteExcellent info ............
ReplyDeletewhat is data structure and its types
Did you know that you can create short links with AdFocus and make money for every visit to your short links.
ReplyDeletecan i get code for constructing a complete Binary search tree using arrays?
ReplyDeleteUseful description
ReplyDeleteNicely explained
ReplyDeleteBinary trees are a form of hierarchical chart like a org chart. Only different is the data and the way data is handled.
ReplyDeleteRegards,
Shalin @ Creately Org Chart Software
Very useful post.
ReplyDeleteRouterlogin
Routerlogin Net