Expression tree

Trees are used in many other ways in the computer science. Compilers and database are two major examples in this regard. In case of compilers, when the languages are translated into machine language, tree-like structures are used. We have also seen an example of expression tree comprising the mathematical expression. Let’s have more discussion on the expression trees. We will see what are the benefits of expression trees and how can we build an expression tree. Following is the figure of an expression tree.

In the above tree, the expression on the left side is a + b * c while on the right side, we have d * e + f * g. If you look at the figure, it becomes evident that the inner nodes contain operators while leaf nodes have operands. We know that there are two types of nodes in the tree i.e. inner nodes and leaf nodes. The leaf nodes are such nodes which have left and right subtrees as null. You will find these at the bottom level of the tree. The leaf nodes are connected with the inner nodes. So in trees, we have some inner nodes and some leaf nodes.

In the above diagram, all the inner nodes (the nodes which have either left or right child or both) have operators. In this case, we have + or * as operators. Whereas leaf nodes contain operands only i.e. a, b, c, d, e, f, g. This tree is binary as the operators are binary. We have discussed the evaluation of postfix and infix expressions and have seen that the binary operators need two operands. In the infix expressions, one operand is on the left side of the operator and the other is on the right side. Suppose, if we have + operator, it will be written as 2 + 4. However, in case of multiplication, we will write as 5*6. We may have unary operators like negation (-) or in Boolean expression we have NOT. In this example, there are all the binary operators. Therefore, this tree is a binary tree. This is not the Binary Search Tree. In BST, the values on the left side of the nodes are smaller and the values on the right side are greater than the node. Therefore, this is not a BST. Here we have an expression tree with no sorting process involved.

This is not necessary that expression tree is always binary tree. Suppose we have a unary operator like negation. In this case, we have a node which has (-) in it and there is only one leaf node under it. It means just negate that operand.

Let’s talk about the traversal of the expression tree. The inorder traversal may be executed here.

We use the inorder routine and give the root of this tree. The inorder traversal will be a+b*c+d*e+f*g. You might have noted that there is no parenthesis. In such expressions when there is addition and multiplication together, we have to decide which operation should be performed first. At that time, we have talked about the operator precedence. While converting infix expression into postfix expression, we have written a routine, which tells about the precedence of the operators like multiplication has higher precedence than the addition. In case of the expression 2 + 3 * 4, we first evaluate 3 * 4 before adding 2 to the result. We are used to solve such expressions and know how to evaluate such expressions. But in the computers, we have to set the precedence in our functions.

We have an expression tree and perform inorder traversal on it. We get the infix form of the expression with the inorder traversal but without parenthesis. To have the parenthesis also in the expressions, we will have to do some extra work.

Here is the code of the inorder routine which puts parenthesis in the expression.

/* inorder traversal routine using the parenthesis */ void inorder(TreeNode<int>* treeNode) { if( treeNode != NULL ){ cout << "("; inorder(treeNode->getLeft()); cout << ")"; cout << *(treeNode->getInfo()); cout << "("; inorder(treeNode->getRight()); cout << ")"; } }

This is the same inorder routine used by us earlier. It takes the root of the tree to be traversed. First of all, we check that the root node is not null. In the previous routine after the check, we have a recursive call to inorder passing it the left node, print the info and then call the inorder for the right node. Here we have included parenthesis using the cout statements. We print out the opening parenthesis ‘(‘before the recursive call to inorder. After this, we close the parenthesis. Then we print the info of the node and again have opening parenthesis and recursive call to inorder with the right node before having closing parenthesis in the end. You must have understood that we are using the parenthesis in a special order. We want to put the opening parenthesis before the start of the expression or sub expression of the left node. Then we close the parenthesis. So inside the parenthesis, there is a sub expression.

On executing this inorder routine, we have the expression as ( a + ( b * c )) + ((( d * e ) + f ) * g ).

We put an opening parenthesis and start from the root and reach at the node ‘a’. After reaching at plus (+), we have a recursive call for the subtree *. Before this recursive call, there is an opening parenthesis. After the call, we have a closing parenthesis. Therefore the expression becomes as (a + ( b * c )). Similarly we recursively call the right node of the tree. Whenever, we have a recursive call, there is an opening parenthesis. When the call ends, we have a closing parenthesis. As a result, we have an expression with parenthesis, which saves a programmer from any problem of precedence now.

Here we have used the inorder traversal. If we traverse this tree using the postorder mode, then what expression we will have? As a result of postorder traversal, there will be postorder expression.

This is the same tree as seen by us earlier. Here we are performing postorder traversal. In the postorder, we print left, right and then the parent. At first, we will print a. Instead of printing +, we will go for b and print it. This way, we will get the postorder traversal of this tree and the postfix expression of the left side is a b c * + while on the right side, the postfix expression is d e * f + g * +. The complete postfix expression is a b c * + d e * f + g * +. The expression undergoes an alteration with the change in the traversal order. If we have some expression tree, there may be the infix, prefix and postfix expression just by traversing the same tree. Also note that in the postfix form, we do not need parenthesis.

Let’s see how we can build this tree. We have some mathematical expressions while having binary operators. We want to develop an algorithm to convert postfix expression into an expression tree. This means that the expression should be in the postfix form. In the start of this course, we have seen how to covert an infix expression into postfix expression. Suppose someone is using a spreadsheet program and typed a mathematical expression in the infix form. We will first convert the infix expression into the postfix expression before building expression tree with this postfix expression.

We already have an expression to convert an infix expression into postfix. So we get the postfix expression. In the next step, we will read a symbol from the postfix expression. If the symbol is an operand, put it in a tree node and push it on the stack. In the postfix expression, we have either operators or operands. We will start reading the expression from left to right. If the symbol is operand, make a tree node and push it on the stack. How can we make a tree node? Try to memorize the treeNode class. We pass it some data and it returns a treeNode object. We insert it into the tree. A programmer can also use the insert routine to create a tree node and put it in the tree.

Here we will create a tree node of the operand and push it on the stack. We have been using templates in the stack examples. We have used different data types for stacks like numbers, characters etc. Now we are pushing treeNode on the stack. With the help of templates, any kind of data can be pushed on the stack. Here the data type of the stack will be treeNode. We will push and pop elements of type treeNode on the stack. We will use the same stack routines.

If symbol is an operator, pop two trees from the stack, form a new tree with operator as the root and T1 and T2 as left and right subtrees and push this tree on the stack. We are pushing operands on the stacks. After getting an operator, we will pop two operands from the stack. As our operators are binary, so it will be advisable to pop two operands. Now we will link these two nodes with a parent node. Thus, we have the binary operator in the parent node.

Let’s see an example to understand it. We have a postfix expression as a b + c d e + * *. If you are asked to evaluate it, it can be done with the help of old routine. Here we want to build an expression tree with this expression. Suppose that we have an empty stack. We are not concerned with the internal implementation of stack. It may be an array or link list.

First of all, we have the symbol a which is an operand. We made a tree node and push it on the stack. The next symbol is b. We made a tree node and pushed it on the stack. In the below diagram, stack is shown.

Our stack is growing from left to right. The top is moving towards right. Now we have two nodes in the stack. Go back and read the expression, the next symbol is + which is an operator. When we have an operator, then according to the algorithm, two operands are popped. Therefore we pop two operands from the stack i.e. a and b. We made a tree node of +. Please note that we are making tree nodes of operands as well as operators. We made the + node parent of the nodes a and b. The left link of the node + is pointing to a while right link is pointing to b. We push the + node in the stack.

Actually, we push this subtree in the stack. Next three symbols are c, d, and e. We made three nodes of these and push these on the stack.

Next we have an operator symbol as +. We popped two elements i.e. d and e and linked the + node with d and e before pushing it on the stack. Now we have three nodes in the stack, first + node under which there are a and b. The second node is c while the third node is again + node with d and e as left and right nodes.

The next symbol is * which is multiplication operator. We popped two nodes i.e. a subtree of + node having d and e as child nodes and the c node. We made a node of * and linked it with the two popped nodes. The node c is on the left side of the * node and the node + with subtree is on the right side.

The last symbol is the * which is an operator. The final shape of the stack is as under:

In the above figure, there is a complete expression tree. Now try to traverse this tree in the inorder. We will get the infix form which is a + b * c * d + e. We don’t have parenthesis here but can put these as discussed earlier.

This is the way to build an expression tree. We have used the algorithm to convert the infix form into postfix form. We have also used stack data structure. With the help of templates, we can insert any type of data in the stack. We have used the expression tree algorithm and very easily built the expression tree.

In the computer science, trees like structures are used very often especially in compilers and processing of different languages.

 

Technorati Tags: ds tutorial,data structure tutorial,tree data structure,trees in data structure,tree ds,tree traversal data structure,tree types,expression trees

Deletion in AVL Tree

 

The deletion of a data item from a data structure has always been difficult whatever data structure we use. The deletion is the inverse of insertion. In deletion there is a given value x and an AVL tree T. We delete the node containing the value x and rebalance the tree if it becomes unbalance after deleting the node. We will see that the deletion of a node is considerably more complex than the insertion of a node. It is complex in the sense that we may have to do more than one rotations to rebalance the tree after deleting a node. We will discuss the deletion case by case and will see that about what points we have to take care in the deletion process.

We are not going to write the code for deletion here. If we have to use AVL tree routines or class, the deletion and insertion routines of AVL tree are available in standard library. We can use these routines in our program. We have no need to write these routines. But here we discuss these to understand their functionality.

We know that insertion in a height-balanced tree requires at most one single rotation or one double rotation. We do this rotation at the node whose balance violates the AVL condition. We can use rotations to restore the balance when we do a deletion. If the tree becomes unbalance after deleting a node then we use rotations to rebalance it. We may have to do a rotation at every level of the tree. Thus in the worst case of deletion we have to do log₂ N rotations. As log₂ N is the number of levels of a tree of N nodes.

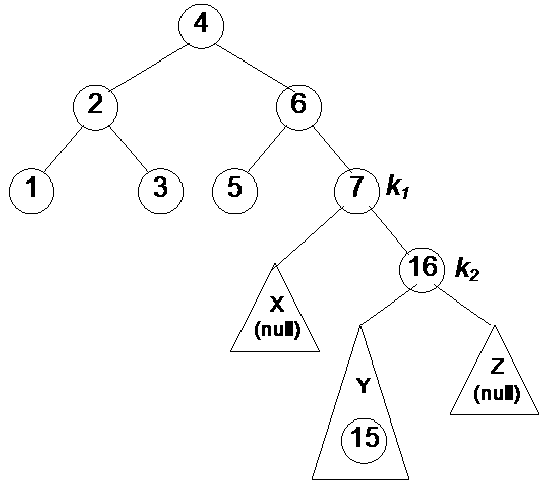
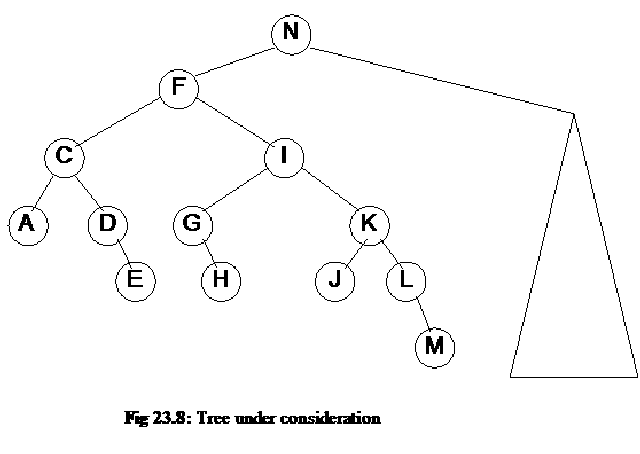
Let’s consider an example of deleting a node from a tree. In this example, we will discuss the worst case of deletion that is we have to do rotation at each level after deleting a node. Look at the following figure i.e. Fig 23.8. In this figure the root of the tree is node N and we have expanded only the left subtree of this node. The right subtree of it is indicated by a triangle. We focus on the left subtree of N. The balance of each non-leaf node of the left subtree of N is –1. This means that at every non-leaf node the depth/height of left subtree is one shorter than the height of right subtree. For example look at the node C. The left subtree of C is one level deep where as it’s right subtree is two levels deep. So balance of it is 1 – 2 = -1. If we look at node I its left subtree has height 2 as there are two levels where nodes G and H exists. The right subtree of I has number of levels (i.e. height) 3 where exists the nodes K, L and M respectively. Thus the balance of I is 2 – 3 = -1. Similarly we can see that other nodes also have the balance –1. This tree is shown in the following figure.

Here in this tree, the deletion of node A from the left subtree causes the worst case of deletion in the sense that we have to do a large number of rotations. Now we delete the node A from the tree. The effect of this deletion is that if we consider the node C the height of its left subtree is zero now. The height of the right subtree of C is 2. Thus the balance of C is 2 now. This makes the tree unbalance. Now we will do a rotation to make the tree balanced. We rotate the right subtree of C that means the link between C and D so that D comes up and C goes down. This is mentioned in the figure below.

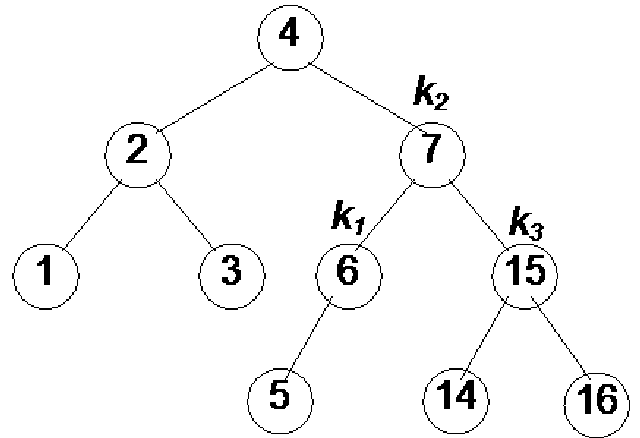
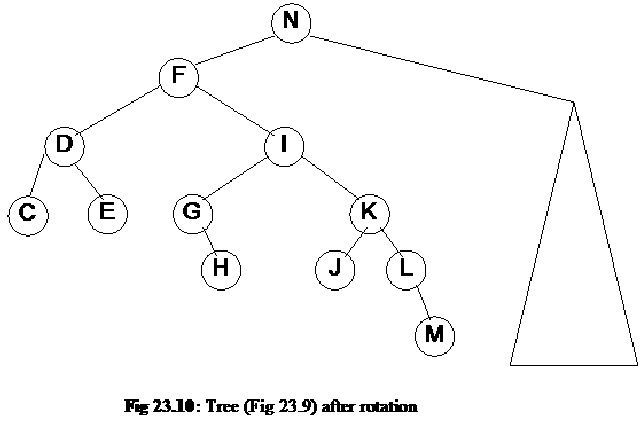
After this rotation the tree has transformed into the following figure. Now D becomes the left child of F and C becomes the left child of D.

By looking at the inorder traversal of the tree, we notice that it is preserved. The inorder traversal of the tree before rotation (i.e. fig 23.8) is C D E F G H I J K L M N. Now if we traverse the tree after rotation (i.e. fig 23.9) by inorder traversal we get C D E F G H I J K L M N, which is the same as it was before rotation.

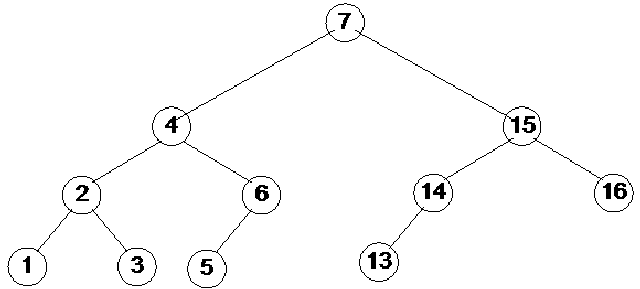
After this rotation we see that the tree having D as root is balanced. But if we see the node F we notice that the height of its left subtree is 2 and height of its right subtree is 4. Thus the balance of F is –2 (or 2 if we take the absolute value) now. Thus the tree becomes unbalance. So we have to do rotation again to balance the tree. The whole left subtree of F is shorter so we do the left rotation on the link of F and I (in the tree in fig 23.9) to bring F down and I up so that the difference of height could be less. After rotation the tree gets the new form that is shown in the figure below.

Here we see that the nodes G and H, which were in the left subtree of I, now become the right subtree of F. We see that the tree with I as root is balanced now. Now we consider the node N. We have not expanded the right subtree of N. Although we have not shown but there may be nodes in the right subtree of N. If the difference of heights of left and right subtree of N is greater than 1 then we have to do rotation on N node to balance the tree.

Thus we see that there may be such a tree that if we delete a node from it we have to do rotation at each level of the tree. We notice that we have to do more rotations in deletion as compared to insertion. In deletion when we delete a node we have to check the balance at each level up to the root. We do rotation if any node at any level violates the AVL condition. If nodes at a level do not violate AVL condition then we do not stop here we check the nodes at each level and go up to the root. We know that a binary tree has log₂ N levels (where N is total number of nodes) thus we have to do log₂ N rotations. We have to identify the required rotations that mean we have to identify that which one rotation out of the four rotations (i.e. single left rotation, single right rotation, double right-left rotation and double left-right rotation) we have to do. We have to identify this at each level.

We can summarize the deletion procedure as under.

Delete the node as in binary search tree. We have seen in the discussion of deleting a node from a BST that we have three cases, which we discussed as follows

Case I: The node to be deleted is the leaf node i.e. it has no right or left child. It is very simple to delete such node. We make the pointer in the parent node pointing to this node as NULL. If the memory for the node has been dynamically allocated, we will release it.

Case II: The node to be deleted has either left child (subtree) or right child (subtree).

In this case we bypass the node in such a way that we find the inorder successor of this node and then link the parent of the node to be deleted to this successor node. Thus the node was deleted.

Case III: The node to be deleted has both the left and right children (subtree). This is the most difficult case. In this case we find the inorder successor of the node. The left most node of the right subtree will be the inorder successor of it. We put the value of that inorder successor node into the node to be deleted. After it we delete the inorder successor node recursively.

In deletion in AVL tree, we delete the node as we delete it in a BST. In third case of deletion in BST we note that the node deleted will be either a leaf or have just one subtree (that will be the right subtree as node deleted is the left most subtree so it cannot have a left subtree). Now we are talking about deletion in an AVL tree. Since this is an AVL tree so if the deleted node has one subtree that subtree contains only one node. Why it is so? Think about its reason and answer.

After deleting the node we traverse up the tree from the deleted node checking the balance of each node at each level up to the root. Thus the deletion in AVL tree is like the deletion in BST except that here in AVL tree we have to rebalance the tree using rotations.

Cases of Deletion in AVL Tree

Now let’s consider the cases of deletion that will help to identify what rotation will be applied at what point.

There are 5 cases to consider. Let’s go through the cases graphically and determine what actions are needed to be taken. We will not develop the C++ code for deleteNode in AVL tree. This is left as an exercise.

Case 1a:

The first case is that the parent of the deleted node had a balance of 0 and the node was deleted in the parent’s left subtree.

In the following figure (Fig 23.12) the left portion shows the parent node with a horizontal line in it. This horizontal line indicates that the left and right subtrees of this node have the same heights and thus the balance of this node is 0. When we delete a node from its left subtree then height of its right subtree becomes larger than the left subtree. The right portion in the figure shows this. We are showing a symbol instead of balance of node inside the node. The notation (symbol) in the node indicates that the height of left subtree is shorter than the height of right subtree of the node.

Now the action that will be taken in this case is that, change the balance of the parent node and stop. No further effect on balance of any higher node. There is no need of rotation in this case. Thus it is the easiest case of deletion.

Let’s consider an example to demonstrate the above case.

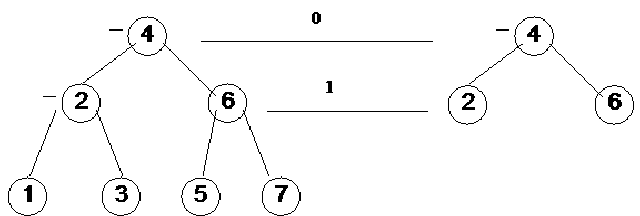
Consider the tree shown in the following figure i.e. Fig 23.13. This is a perfectly balanced tree. The root of this tree is 4 and nodes 1, 2 and 3 are in its left subtree. The nodes 5, 6 and 7 are in the right subtree.

Consider the node 2. We have shown the balance of this node with a horizontal line, which indicates that the height of its left subtree is equal to that of its right subtree. Similarly we have shown the balance of node 4.

Now we remove the node 1 which is the left subtree of node 2. After removing the left child (subtree) of 2 the height of left subtree of 2 is 0. The height of right subtree of 2 is 1 so the balance of node 2 becomes –1. This is shown in the figure by placing a sign that is down ward to right side, which indicates that height of right subtree is greater than left subtree. Now we check the node 4. Here the height of left subtree of it is still 2. The height of its right subtree is also 2. So balance of the node 4 is 0 that is indicated by the small horizontal line (minus sign) in the figure below. Here we don’t need to change the balance of 4.

Fig 23.14: Tree before and after deleting node 1

Case 1b:

This case is symmetric to case 1a. In this case, the parent of the deleted node had a balance of 0 and the node was deleted in the parent’s right subtree. The following figure shows that the balance of the node was zero as left and right subtree of it have the same heights.

After removing the right child the balance of it changes and it becomes 1, as the height of its left subtree is 1 greater than the height of right subtree. The action performed in this case is the same as that in case 1a. That is change the balance of the parent node and stop. No further effect on balance of any higher node.

The previous example can be done for this case only with the change that remove the right child of node 2 i.e. 3.

Case 2a:

This is the case where the parent of the deleted node had a balance of 1 and the node was deleted in the parent’s left subtree. This means that the height of left subtree of the parent node is 1 greater than the height of its right subtree. It is shown in the left portion of the figure below.

Now if we remove a node from the left subtree of this node then the height of left subtree will decrease by 1 and get equal to the height of right subtree. Thus the balance of this node will be zero. In this case, the action that we will perform to balance the tree is that change the balance of the parent node. This deletion of node may have caused imbalance in higher nodes. So it is advised to continue up to the root of the tree. We will do rotation wherever the balance of the node violates the AVL condition.

There are five cases to consider while deleting a node of an AVL tree. When a node is deleted, the tree can become unbalanced. We calculate the balance factor of each node and perform rotation for unbalanced nodes. But this rotation can prolong to the root node. In case of insertion, only one node’s balance was adjusted as we saw in previous lectures but in case of deletion, this process of rotation may expand to the root node. However, there may also be cases when we delete a node and perform no or one rotation only.

Now, we will see the five cases of deletion. A side note is that we are not going to implement these cases in C++ in this lecture, you can do it yourself as an exercise with the help of the code given inside your text book. In this lecture, the emphasis will be on the deletion process and what necessary actions we take when a node is required to be deleted from an AVL tree. Actually, there are two kinds of actions taken here, one is deletion and the other one is the rotation of the nodes.

Case 1a: The parent of the deleted node had a balance of 0 and a node was deleted in the parent’s left subtree.

In the left tree in the Fig 24.1, the horizontal line inside the tree node indicates that the balance is 0, the right and left subtrees of the node are of equal levels. Now, when a node is deleted from the left subtree of this node, this may reduce by one level and cause the balance of the right subtree of the node to increase by 1 relatively. The balance of the node in favor of the right subtree is shown by a triangular knob tilted towards right. Now, the action required in this case to make the tree balanced again is:

Change the balance of the parent node and stop. There is no further effect on balance of any higher node.

In this case, the balance of the tree is changed from 0 to –1, which is within the defined limits of AVL tree, therefore, no rotation is performed in this case.

Below is a tree in which the height of the left subtree does not change after deleting one node from it.

The node 4 is the root node, nodes 2 and 6 are on level 1 and nodes 1, 3, 5, 7 are shown on level 2. Now, if we delete the node 1, the balance of the node 2 is tilted towards right, it is –1. The balance of the root node 4 is unchanged as there is no change in the number of levels within right and left subtrees of it. Similarly, there is no change in the balances of other nodes. So we don’t need to perform any rotation operation in this case.

Let’s see the second case.

Case 1b: the parent of the deleted node had a balance of 0 and the node was deleted in the parent’s right subtree.

On the left of Fig 24.3, the tree is within the balance limits of AVL. After a node is deleted from the right subtree of it. The balance of the tree is tilted towards left as shown in the right tree show in the Fig 24.3. Now, we see what action will be required to make the tree balanced again.

Change the balance of the parent node and stop. No further effect on balance of any higher node (same as 1a).

So in this case also, we don’t need to perform rotation as the tree is still an AVL (as we saw in the Case 1a). It is important to note that in both of the cases above, the balance of the parent node was 0. Now, we will see the cases when the balance of the parent node is not 0 previously.

Case 2a: The parent of the deleted node had a balance of 1 and the node was deleted in the parent’s left subtree.

In the Fig 24.4 above, the tree on the left contains the balance factor as 1, which means that the left subtree of the parent node is one level more than the number of levels in the right subtree of it. When we delete one node from the left subtree of the node, the height of the left subtree is changed and the balance becomes 0 as shown in the right side tree of Fig 24.4. But it is very important understand that this change of levels may cause the change of balance of higher nodes in the tree i.e.

Change the balance of the parent node. May have caused imbalance in higher nodes so continue up the tree.

So in order to ensure that the upper nodes are balanced, we calculate their balance factors for all nodes in higher levels and rotate them when required.

Case 2b: The parent of the deleted node had a balance of -1 and the node was deleted in the parent’s right subtree.

Similar to the Case 2a, we will do the following action:

Change the balance of the parent node. May have caused imbalance in higher nodes so continue up the tree.

Now, we see another case.

Case 3a:The parent had balance of -1 and the node was deleted in the parent’s left subtree, right subtree was balanced.

As shown in the left tree in Fig 24.5, the node A is tilted towards right but the right subtree of A (node B above) is balanced. The deleted node lies in the left subtree of the node A. After deletion, the height of the left subtree is changed to h-1 as depicted in the right tree of above figure. In this situation, we will do the following action:

Perform single rotation, adjust balance. No effect on balance of higher nodes so stop here.

After single left rotation, we have the tree as shown in the figure below.

Node A has become the left subtree of node B and node 2 left subtree of node B has become the right subtree of node A. The balance of node B is tiled towards left and balance of node A is tilted towards right but somehow, both are within AVL limits. Hence, after a single rotation, the balance of the tree is restored in this case.

Case 4a: Parent had balance of -1 and the node was deleted in the parent’s left subtree, right subtree was unbalanced.

In the last case 3a, the right subtree of node A was balanced. But in this case, as shown in the figure above, the node C is tilted towards left. The node to be deleted lies in the left subtree of node A. After deleting the node the height of the left subtree of node A has become h-1. The balance of the node A is shown tilted towards right by showing two triangular knobs inside node A. So what is the action here.

Double rotation at B. May have affected the balance of higher nodes, so continue up the tree.

By performing double rotation in the tree above, we have the following tree.

Node A, which was the root node previously, has become the left child of the new root node B. Node C, which was the right child of the root node C has now become the right child of the new root node B.

Case 5a: The parent had balance of -1 and the node was deleted in the parent’s left subtree, right subtree was unbalanced.

In the figure above, the right tree of the node B has a height of h-1 while the right subtree is of height h. When we remove a node from the left subtree of node A, the new tree is shown on the right side of Fig 24.9. The subtree 1 has height h-1 now, while subtrees 2 and 3 have the same heights. So the action we will do in this case is:

Single rotation at B. May have effected the balance of higher nodes, so continue up the tree.

These were the five cases of deletion of a node from an AVL tree. Until now, we are trying to understand the concept using the figures. You might have noticed the phrase ‘continue up the tree’ in the actions above. How will we do it? One way is to maintain the pointer of the parent node inside each node. But often the easiest method when we go in downward direction and then upward is recursion. In recursion, the work to be done later is pushed on to the stack and we keep on moving forward until at a certain point we back track and do remaining work present in the stack. We delete a node when we reach at the desired location and then while traversing back, do the rotation operation on our way to the root node.

Symmetrical to case 2b, we may also have cases 3b, 4b and 5b. This should not be a problem in doing it yourself.

Other Uses of Binary Trees

A characteristic of binary trees is that the values inside nodes on the left of a node are smaller than the value in the node. And the values inside the nodes on the right of a node are greater than the value in the node. This is the way a binary tree is constructed.

Whatever is the size of the tree, the search is performed after traversing upto log₂n levels maximum.

We have observed that the binary tree becomes a linked list and it can become shallow. The AVL conditions came into picture to control the height balance of a binary tree. While searching in an AVL tree, in the worst case scenario we have to search 1.44 log₂n levels. For searches, binary and AVL trees are the most efficient but we do have some other kinds of trees that will be studied later.

Lets see what could be some other uses of binary trees, we start our discussion with Expression Trees.

Expression Trees

Expression trees, the more general parse trees and abstract syntax trees are significant components of compilers.

We already know about compilers that whenever we write our program or code in some computer language like C++ or Java. These programs are compiled into assembly language or byte code (in case of Java). This assembly language code is translated converted into machine language and an executable file is made by another program called the assembler.

By the way, if you have seen your syllabus, you might have seen that there is a dedicated subject on compilers. We study in detail about compilers in that course. For this course, we will see expression or parse trees.

We will take some examples of expression trees and we will not delve into much depth of it rather that would be an introduction to expression trees.

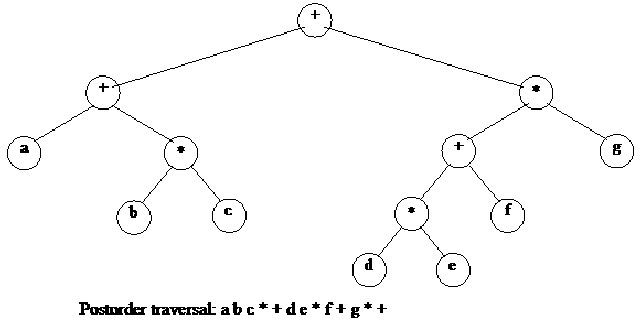
You can see the infix expression above (a + b * c) + ( (d * e + f) * g), it is represented in the tree form also.

You can see from bottom of the tree that the nodes b and c in the nodes are present at the same level and their parent node is multiplication (*) symbol. From the expression also, we see that the b and c are being multiplied. The parent node of a is + and right subtree of + is b*c. You might have understood already that this subtree is depicting a+b*c. On the right side, node d and e are connected to the parent *. Symbol + is the parent of * and node f. The expression of the subtree at node + is d*e+f. The parent of node + is * node, its right subtree is g. So expression of the subtree at this node * is (d*e+f)*g). The root node of the tree is +.

These expression trees are useful in compilers and in spreadsheets also, they are sometimes called parse trees.

Parse Tree in Compilers

See the expression tree of expression A := A + B * C below. We are adding B and C, adding the resultant in A and then finally assigning the resultant to A.

The root node in the parse tree shown above is <assign>.

The assignment statement (<assign>) has three parts. On the left of it, there is always an identifier (single or an array reference) called l-value. The l-value shown in the tree above is <id> and the identifier is A in the expression above. The second part of assignment statement is assignment operator (= or :=). One the right of assignment operator lies the third part of assignment statement, which is an expression. In the expression A := A + B * C above , the expression after assignment operator is A + B * C. In the tree, it is represented by the node <expr>. The node <expr> has three subnodes: <expr>, + and <term>. <expr>’s further left subtree is <expr>, <term>, <factor>, <id> and then finally is B. The right subchild <term> has further subnodes as <term>, * and <factor>. <factor> has <id> as subchild and <id> has C.

Note the nodes in gray shade in the tree above form A = A + B * C.

Compiler creates these parse trees. We will see how to make these trees, when we will parse any language tree like C++. Parsing mean to read and then extract the required structure. A compiler parses a computer language like C++ to form parse trees. Similarly, when we do speech recognition. Each sentence is broken down into a certain structure in form of a tree. Hand writing recognition also involves this. The tablet PCs these days has lot of implementation of parse trees.

Parse Tree for an SQL Query

Let’s see another example of parse trees inside databases. The parse trees are used in query processing. The queries are questions to the databases to see a particular kind of data. Consider you have a database for a video store that contains data of movies and artists etc. You are querying that database to find the titles of movies with stars born in 1960. The language used to query from the database is called SQL (Structured Query Language), this language will be dealt in depth in the databases course. The tables lying in this movies database are:

StarsIn(title, year, starName)

MovieStar(name, address, gender, birthdate)

The following SQL query is used to retrieve information from this database:

SELECT title

FROM StarsIn, MovieStar

WHERE starName = name AND birthdate LIKE ‘%1960’ ;

This query is asking to retrieve the titles of those movies from StarsIn and MovieStar tables where the birthdate of an actor is 1960. We see in query processing a tree is formed as shown in the figure below:

The root node is Query. This node is further divided into SELECT, <SelList>, FROM, <FromList>, WHERE and <Condition> subnodes. <SelList> will be an Attribute and finally a title is reached. Observe the tree figure above, how the tree is expanded when we go in the downward direction. When the database engine does the query process, it makes these trees. The database engine also performs query optimization using these trees.

Compiler Optmization

Let’s see another expression tree here:

The root node is +, left subtree is capturing the f+d*e expression while the right subtree is capturing (d*e+f)*g.

Normally compilers has intelligence to look at the common parts inside parse trees. For example in the tree above, the expressions f+d*e and d*e+f are same basically. These common subtrees are called common subexpressions. To gain efficiency, instead of calculating the common subexpressions again, the compilers calculates them once and use them at other places. The part of the compiler that is responsible to do this kind of optimization is called optimizer.

See the figure below, the optimizer (part of compiler) will create the following graph while performing the optimization. Because both subtrees were equivalent, it has taken out one subtree and connected the link from node * to node +.

This figure is not a tree now because it has two or more different paths to reach a node. Therefore, this has become a graph. The new connection is containing a directed edge, which is there in graphs.

Optimizer uses the expressions trees and converts them to graphs for efficiency purposes. You read out from your book, how the expression trees are formed, what are the different methods of creating them.

 

Technorati Tags: ds tutorial,data structure tutorial,tree data structure,trees in data structure,tree ds,tree traversal data structure,tree types,types of trees,binary trees,binary search trees,bst,bst data structure,bst ds,complete binary search tree,non tree structure,linear tree,avl tree,avl tree traversal,avl data structure,avl ds,avl tree rotation,rotation of avl tree,avl tree tutorial,expression trees

Cases of Rotation of AVL Tree

 

The single rotation does not seem to restore the balance. We will re-visit the tree and rotations to identify the problem area. We will call the node that is to be rotated as a (node requires to be re-balanced). Since any node has at the most two children, and a height imbalance requires that a’s two sub-trees differ by two (or –2), the violation will occur in four cases:

1. An insertion into left subtree of the left child of a.

2. An insertion into right subtree of the left child of a.

3. An insertion into left subtree of the right child of a.

4. An insertion into right subtree of the right child of a.

The insertion occurs on the outside (i.e., left-left or right-right) in cases 1 and 4. Single rotation can fix the balance in cases 1 and 4.

Insertion occurs on the inside in cases 2 and 3 which a single rotation cannot fix.

Let’s see the figure below:

We have shown, single right notation to fix case 1. Two nodes k2 and k1 are shown in the figure, here k2 is the root node (and also the a node, k1 is its left child and Z shown in the triangle is its right child. The nodes X and Y are the left and right subtrees of the node k1. A new node is also shown below to the triangle of the node X, the exact position (whether this node will be right or left child of the node X) is not mentioned here. As the new node is inserted as a child of X that is why it is called an outside insertion, the insertion is called inside if the new node is inserted as a child of the node Y. This insertion falls in case 1 mentioned above, so by our definition above, single rotation should fix the balance. The k2 node has been rotated single time towards right to become the right child of k1 and Y has become the left child of k2. If we traverse the tree in inorder fashion, we will see that the output is same:

X k1 Y k2 Z

Consider the the figure below:

In this figure (Fig 21.14), the new node has been inserted as a child node of Z, that is why it is shown in bigger size covering the next level. Now this is an example of case 4 because the new node is inserted below the right subtree of the right child of the root node (a). One rotation towards should make it balanced within limits of AVL tree. The figure on the right is after rotation the node k1 one time towards left. This time node Y has become the right child node of the node k1.

In our function of insertion in our code, we will do insertion, will compute the balance factors for nodes and make rotations.

Now, we will see the cases 2 and 3, these are not resolved by a single rotation.

We see here that the new node is inserted below the node Y. This is an inside insertion. The balance factor for the node k2 became 2. We make single rotation by making right rotation on the node k2 as shown in the figure on the right. We compute the balance factor for k1, which is –2. So the tree is still not within the limits of AVL tree. Primarily the reason for this failure is the node Y subtree, which is unchanged even after making one rotation. It changes its parent node but its subtree remains intact. We will cover the double rotation in the next lecture.

It is very important that you study the examples given in your text book and try to practice the concepts rigorously.

Now the question arises whether the single rotation help us in balancing the tree or not. If the new node is inserted in the left subtree of the a’s left child or in the right subtree of a’s right child, the balance will be restored through single rotation. However, if the new node goes inside the tree, the single rotation is not going to be successful in balancing the tree.

We face four scenarios in this case. We said that in the case-1 and case-4, single rotation is successful while in the case-2 and case-3 single rotation does not work. Let’s see the tree in the diagram given below.

In the above tree, we have a node as k2, which has a left child as k1. Whereas X and Y are its left and right children. The node k2 has a right child Z. Here the newly inserted node works as the left or right child of node Y. Due to this insertion, one level is increased in the tree. We have applied single rotation on the link of k1 and k2. The right side tree in the figure is the post-rotation tree. The node k1 is now at the top while k2 comes down and node Y changes its position. Now if you see the levels of the node, these are seen same. Have a look on the level of the a node i.e. k1 which reflects that the difference between the left and right side levels is still 2. So the single rotation does not work here.

Let’s see how we can fix that problem. A fresh look on the following diagram will help us understand the problem.

Here k2 is the root node while k1 and Z are the right and left children respectively. The new node is inserted under Y so we have shown Y in a big triangle. The new node is inserted in the right subtree of k1, increasing its level by 1. Y is not empty as the new node was inserted in it. If Y is empty, the new node will be inserted under k1. It means that Y has a shape of a tree having a root and possibly left and right subtrees. Now view the entire tree with four subtrees connected with 3 nodes. See the diagram below.

We have expanded the Y and shown the root of Y as K2, B and C are its left and right subtrees. We have also changed the notations of other nodes. Here, we have A, B, C and D as subtrees and k1, k2 and k3 as the nodes. Let’s see where the new node is inserted in this expanded tree and how can we restore its balance. Either tree B or C is two levels deeper than D. But we are not sure which one is deeper. The value of new node will be compared with the data in k2 that will decide that this new node should be inserted in the right subtree or left subtree of the k2. If the value in the new node is greater than k2, it will be inserted in the right subtree i.e. C. If the value in the new node is smaller than k2, it will be inserted in the left subtree i.e. B. See the diagram given below:

We have seen the both possible locations of the new node in the above diagram. Let’s see the difference of levels of the right and left subtrees of the k3. The difference of B or C from D is 2. Therefore the expansion of either of B or C, due to the insertion of the new node, will lead to a difference of 2. Therefore, it does not matter whether the new node is inserted in B or C. In both of the cases, the difference becomes 2. Then we try to balance the tree with the help of single rotation. Here the single rotation does not work and the tree remains unbalanced. To re-balance it, k3 cannot be left as the root. Now the question arises if k3 cannot become root, then which node will become root? In the single rotation, k1 and k3 were involved. So either k3 or k1 will come down. We have two options i.e. left rotation or right rotation. If we turn k1 into a root, the tree will be still unbalanced. The only alternative is to place k2 as the new root. So we have to make k2 as root to balance the tree. How can we do that?

If we make k2 the root, it forces k1 to be k2‘s left child and k3 to be its right child. When we carry out these changes, the condition is followed by the inorder traversal. Let’s see the above tree in the diagram. In that diagram, the k3 is the root and k1 is its left child while k2 is the right child of k1. Here, we have A, B, C and D as subtrees. You should know the inorder traversal of this tree. It will be A, k1, B, k2, C, k3 and D where A, B, C and D means the complete inorder traversal of these subtrees. You should memorize this tree traversal.

Now we have to take k2 as the root of this tree and rearrange the subtrees A, B, C and D. k1 will be the left child of k2 while k3 is going to be its right child. Finally if we traverse this new tree, it will be the same as seen above. If it is not same, it will mean that there is something wrong in the rotation. We have to find some other solution. Now let’s see how we can rotate our tree so that we get the desired results.

Left-right double rotation to fix case 2

We have to perform a double rotation to achieve our desired results. Let’s see the diagram below:

On the left side, we have the same tree with k3 as its root. We have also shown the new nodes as new and new’ i.e. the new node will be attached to B or C. At first, we will carry out the left rotation between k1 and k2. During the process of left rotation, the root k1 comes down and k2 goes up. Afterwards, k1 will become the left child of k2 and the left subtree of k2 i.e. B, will become the right subtree of k1. This is the single rotation. You can see the new rotated tree in the above figure. It also shows that the B has become the right child of the k1. Moreover, the new node is seen with the B. Now perform the inorder traversal of this new rotated tree. It is A, k1, B, k2, C, k3 and D. It is same as witnessed in case of the inorder traversal of original tree. With this single rotation, the k2 has gone one step up while k1 has come down. Now k2 has become the left child of k3. We are trying to make the k2 the root of this tree. Now what rotation should we perform to achieve this?

Now we will perform right rotation to make the k2 the root of the tree. As a result, k1 and k2 have become its left and right children respectively. The new node can be inserted with B or C. The new tree is shown in the figure below:

Now let’s see the levels of new and new’. Of these, one is the new node. Here you can see that the levels of new, new’ i.e. A and D are the same. The new tree is now a balanced one. Let’s check the inorder traversal of this tree. It should be the same as that of the original tree. The inorder traversal of new tree is A, k1, B, k2, C, k3 and D, which is same as that of the original tree.

This is known as double rotation. In double rotation, we perform two single rotations. As a result, the balance is restored and the AVL condition is again fulfilled. Now we will see in which order, the double rotation is performed? We performed a left rotation between k1 and k2 link, followed by a right rotation.

Right-left double rotation to fix case 3

In case, the node is inserted in left subtree of the right child, we encounter the same situation as discussed above. But here, we will perform right rotation at first before going for a left rotation. Let’s discuss this symmetric case and see how we can apply double rotation here. First we perform the right rotation.

Here k1 is the root of the tree while k3 is the right child of the k1. k2 is the inner child. It is the Y tree expanded again here and the new node will be inserted in the k2’s right subtree C or left subtree B. As we have to transform the k2 into the root of the tree, so the right rotation between the link k2 and k3 will be carried out. As a result of this rotation, k2 will come up and k3 will go down. The subtree B has gone up with the k2 while subtree C is now attached with the k3. To make the k2 root of the tree, we will perform the left rotation between then k1 and k2. Let’s see this rotation in the figure below:

In the above figure at the right side, we have the final shape of the tree. You can see that k2 has become the root of the tree. k1 and k3 are its left and right children respectively. While performing the inorder traversal, you will see that we have preserved our inorder traversal.

We have started this activity while building an example tree. We inserted numbers in it. When the balance factor becomes more than one, rotation is performed. During this process, we came at a point when single rotation failed to balance the tree. Now there is need to perform double rotation to balance the tree that is actually two single rotations. Do not take double rotation as some complex function, it is simply two single rotations in a special order. This order depends on the final position of the new node. Either the new node is inserted at the right subtree of the left child of a node or at the left subtree of the right child of a node. In first case, we have to perform left-right rotation while in the second case, the right-left rotation will be carried out.

Let’s go back to our example and try to complete it. So far, we have 1, 2, 3, 4, 5, 6, 7 and 16 in the tree and inserted 15 which becomes the left child of the node 16. See the figure below:

Here we have shown X, Y and Z in case of the double rotation. We have shown Y expanded and 15 is inside it. Here we will perform the double rotation, beginning with the right rotation first.

We have identified the k1, k2 and k3 nodes. This is the case where we have to perform right-left double rotation. Here we want to promote k2 upwards. For this purpose, the right rotation on the link of k2 and k3 i.e. 15 and 16 will be carried out.

The node 15 now comes up while node 16 has gone down. We have to promote k2 to the top and k3 and k1 will become its right and left children respectively. Now we will perform left rotation on the link of k1 and k2 i.e. 7 and 15. With this left rotation, 15 goes up and 7 and 16 become its left and right children respectively.

Here we have to check two things. At first, the tree is balanced or not i.e. the AVL condition is fulfilled or not. Secondly we will confirm that the inorder traversal is preserved or not. The inorder traversal should be the same as that of the inorder traversal of original tree. Let’s check these two conditions. The depth of the left subtree of node 4 is 2 while the depth of the right subtree of node 4 is three. Therefore, the difference of the levels at node 4 is one. So the AVL condition is fulfilled at node 4. At node 6, we have one level on it left side while at the right side of node 6, there are two levels. As the difference of levels is one, therefore node 6 is also balanced according to the AVL condition. Similarly other nodes are also fulfilling the AVL condition. If you see the figure above, it is clear that the tree is balanced.

We are doing all this to avoid the link list structure. Whenever we perform rotation on the tree, it becomes clear from the figure that it is balanced. If the tree is balanced, in case of searching, we will not have to go very deep in the tree. After going through the mathematical analysis, you will see that in the worst case scenario, the height of the tree is 1.44 log₂ n. This means that the searching in AVL is logarithmic. Therefore if there are ten million nodes in an AVL tree, its levels will be roughly as log₂(10 million) which is very few. So the traversal in an AVL tree is very simple.

Let’s insert some more nodes in our example tree. We will perform single and double rotations, needed to make the tree balanced. The next number to be inserted is 14. The position of node 14, according to the inorder traversal, is the right child of 7. Let’s see this in the diagram as:

The new node 14 is inserted as the right child of 7 that is the inner subtree of 15. Here we have to perform double rotation again. We have identified the k1, k2 and k3. k2 has to become the root of this subtree. The nodes k1 and k3 will come down with their subtrees while k2 is going to become the root of this subtree. After the right rotation the tree will be as:

With the right rotation, k2 has come one step up while k3 has been turned into the right child of k2 but k1 is still up. Now we will perform a left rotation on the link of k1 and k2 to make the k2 root of this subtree. Now think that after this rotation and rearrangement of node what will be the shape of the tree.

After the double rotation, the final shape of the tree will be as:

k2 has become the root of the subtree. k1 has attained the role of the left child of k2 and k3 has become the right child of the k2. The other nodes 5, 14 and 16 have been rearranged according to the inorder traversal. The node 7 has come up where as node 6 and 15 have become its left and right child. Now just by viewing the above figure, it is clear that the tree is balanced according to the AVL condition. Also if we find out its inorder traversal, it should be the same as the inorder traversal of original tree. The inorder traversal of the above tree is 1, 2, 3, 4, 5, 6, 7, 14, 15, and 16. This is in sorted order so with the rotations the inorder traversal is preserved.

Let’s insert some more numbers in our tree. The next number to be inserted is 13.

We have to perform single rotation here and rearrange the tree. It will look like as:

The node 7 has become the root of the tree. The nodes 4, 2, 1, 3, 6, 5 have gone to its left side while the nodes 15, 14, 13, 16 are on its right side. Now try to memorize the tree which we build with these sorted numbers. If you remember that it looks like a link list. The root of that tree was 1. After that we have its right child as 2, the right child of 2 as 3, then its right child 4 and so on up to 16. The shape of that tree looks exactly like a linked list. Compare that with this tree. This tree is a balanced one. Now if we have to traverse this tree for search purposes, we have to go at the most three levels.

Now you must be clear why we need to balance the trees especially if we have to use the balanced search trees. While dealing with this AVL condition, it does not matter whether the data, provided to a programmer is sorted or unsorted. The data may be sorted in ascending order or descending order. It may contain alphabets or names in any order. We will keep our tree balanced during the insertion and tree will be balanced at each point. Our tree will not be balanced in the end, it will be balanced with each insertion. It will not be completely balanced. At the maximum, if we pick any node, the difference in the levels of its right subtree and left subtree will not be more than 1.

Now if we have 9 or 10 nodes in the tree and take log of this, it will be near 3. Therefore our tree has three levels after that there are its leaf nodes. Please keep this in mind that originally we have thought BST as an abstract data type. We have defined operations on it like insert, remove and the major method was find. The find method takes a data item and searches the tree. It will also show that this data item exists or not in the tree. We also right findMin and findMax methods. In case of a BST, we can find the minimum and maximum value in it. The minimum will be the left most node of the tree while the right most node of BST will give the maximum value. You can confirm it by applying this on the above tree.

Technorati Tags: ds tutorial,data structure tutorial,tree data structure,trees in data structure,tree ds,tree traversal data structure,tree types,types of trees,binary trees,binary search trees,bst,bst data structure,bst ds,complete binary search tree,non tree structure,linear tree,avl tree,avl tree traversal,avl data structure,avl ds,avl tree rotation,rotation of avl tree,avl tree tutorial