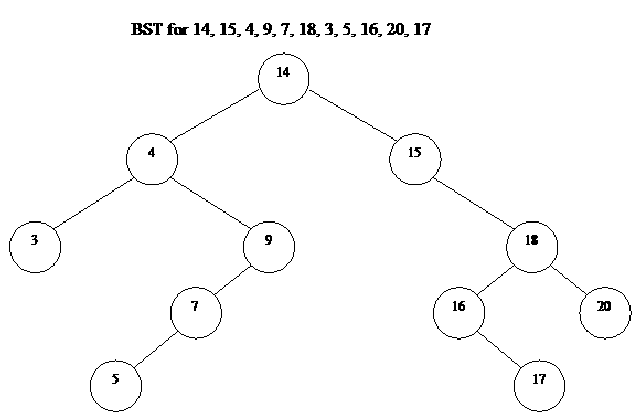
Consider the tree as shown below:
The above tree contains nodes with values as 14, 15, 4, 9, 7, 18, 3, 5, 16, 20, 17 respectively. The root node is 14. The right subtree contains the numbers greater than 14 and the left subtree contains the numbers smaller than 14. This is the property of the binary search tree that at any node, the left subtree contains the numbers smaller than this node and the right subtree contains the numbers greater than this node.
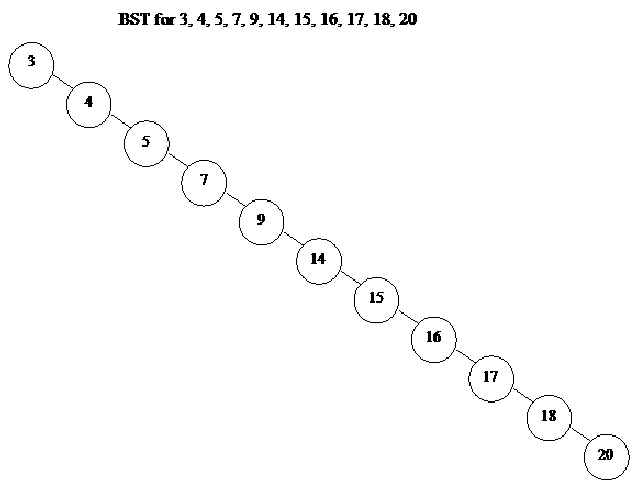
Now suppose that we are given data as 3, 4, 5, 7, 9, 14, 15, 16, 17, 18, 20 to create a tree containing these numbers. Now if our insert method takes the data in the order as given above, what will be the shape of our tree? Try to draw a sketch of the tree with some initial numbers in your mind. The tree will look like:
It does not seem to be a binary tree. Rather, it gives a look of a linked list, as there is a link from 3 to 4, a link from 4 to 5, a link from 5 to 7. Similarly while traversing the right link of the nodes, we reached at the node 20. There is no left child of any node. That’s why, it looks like a link list. What is the characteristic of the link list? In link list, every node has a pointer that points to the next node. While following this pointer, we can go to the next node. The root of this tree is 3. Now we have to find the node with value 20 in this tree. Remember that it is a tree, not a link list. We will use find method to search the number 20 in this tree. Now we will start from the root. As 20 is greater than 3, the recursive call to the method find will be made and we come to the next node i.e. 4. As 20 is greater than 4, so again a recursive call is generated. Similarly we will come to 5, then 7, 9 and so on. In the end, we will reach at 20 and the recursion will stop here.
Now if we search the above tree through the method in which we started from 3, then 4, 5 and so on, this will be the same technique as adopted in the link list. How much time it will take to find the number? We have seen in the link list that if the number to be searched is at the last node, a programmer will have to traverse all the nodes. This means that in case of nodes having strength of n, the loop will execute n times. Similarly as shown in the above tree, our find method will be called recursively equal to number of nodes in the tree. We have designed binary search tree in such a fashion that the search process is very short. You must be remembering the example of previous lecture that if we have one lakh numbers, it is possible to find the desired number in 20 iterations. If we have link list for one lakh elements, the required results can be obtained only after executing the loop for one lakh times if the element to be searched is the last element. However, in case of BST, there are only 20 steps. The BST technique, as witnessed earlier, is quite different as compared to this tree. They have both left and right subtrees. What happened with this tree? The benefit we have due to BST is not applicable here. It seems that it is a link list. This is only due to the fact that the data of the tree was given in the sorted order.
If you want to create a tree out of a sorted data with the insert method, it will look like the above tree. It means that you do not want to have sorted data. But it is not easy, as you might not have control over this process. Consider the example of polling. It is not possible that all the voters come to the polling station in some specific order. But in another example, if you are given a list of sorted data and asked to create a BST with this data. If you create a BST with data that is in an ascending order, it will look like a link list. In the link list, the search takes a lot of time. You have created a BST but the operations on it are working as it is a singly link list. How can we avoid that?
We know that the BST is very beneficial. One way to avoid this is that some how we get the sorted data unsorted. How this can be done. It is not possible, as data is not always provided as a complete set. Data is provided in chunks most of the times. Now what should we do? We will apply a technique here so that we can get the benefits of the BST. We should keep the tree balanced. In the above tree, nodes have left child and no right child. So this tree is not balanced. One way to achieve it is that both the left and right subtrees have the same height. While talking about the binary search tree, we discussed the height, depth and level of BST. Every node has some level. As we go down to the tree from the root, the levels of the tree increased and also the number of nodes, if all the left and right subtrees are present. You have earlier seen different examples of tree. The complete binary tree is such a tree that has all the left and right subtrees and all the leaf nodes in the end. In the complete binary tree, we can say that the number of nodes in the left subtree and right subtree are equal. If we weigh that tree on the balance, from the root, both of its sides will be equal as the number of nodes in the right subtree and left subtree are equal. If you have such a balanced binary search tree with one lakh nodes, there will need of only 20 comparisons to find a number. The levels of this tree are 20. We have also used the formula log2 (100,000). The property of such a tree is that the search comparison can be computed with the help of log because subtrees are switched at every comparison.
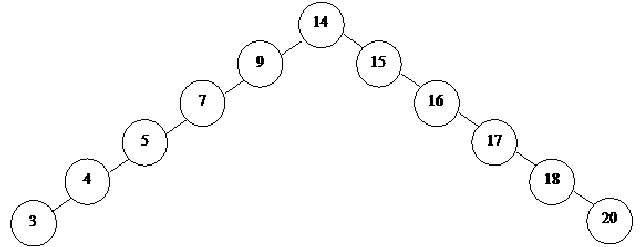
Now let’s see the above tree which is like a singly link list. We will try to convert it into a balanced tree. Have a look on the following figure.
This tree seems to be a balanced tree. We have made 14 as the root. The nodes at the left side occur at the left of all the nodes i.e. left subtree of 14 is 9, the left subtree of 9 is 7, the left subtree of 7 is 5 and so on. Similarly the right subtree contains the nodes 15, 16, 17, 18, 20. This tree seems to be a balanced tree. Let’s see its level. The node 14 i.e. the root is at level zero. Then at level one, we have 9 and 15. At level two, there are 7 and 16. Then 5 and 17, followed by 4 and 18. In the end, we have 3 and 20. It seems that we have twisted the tree in the middle, taking 14 as a root node. If we take other nodes like 9 or 7, these have only left subtree. Similarly if we take 15 or 16, these have right subtrees only. These nodes do not have both right and left subtree. In the earlier example, we have seen that the nodes have right and left subtrees. In that example, the data was not sorted. Here the tree is not shallow. Still we can not get the required BST. What should we do? With the sorted data, the tree can not become complete binary search tree and the search is not optimized. We want the data in unsorted form that may not be available.
We want to make a balanced tree, keeping in mind that it should not be shallow one. We could insist that every node must have left and right subtrees of same height. But this requires that the tree be a complete binary tree. To achieve it, there must be (2d+1 – 1) data items, where d is the depth of the tree. Here we are not pleading to have unsorted data. Rather, we need as much data which could help make a balanced binary tree. If we have a tree of depth d, there will be need of (2d+1 – 1) data items i.e. we will have left and right subtrees of every node with the same height. Now think yourself that is it possible that whenever you build a tree or someone uses your BST class can fulfill this condition. This is not possible that whenever we are going to create a tree, there will be (2d+1 – 1) data items for a tree of depth d. The reason is that most of the time you do not have control over the data. Therefore this is too rigid condition. So this is also not a practical solution.
AVL Tree
AVL tree has been named after two persons Adelson-Velskii and Landis. These two had devised a technique to make the tree balanced. According to them, an AVL tree is identical to a BST, barring the following possible differences:
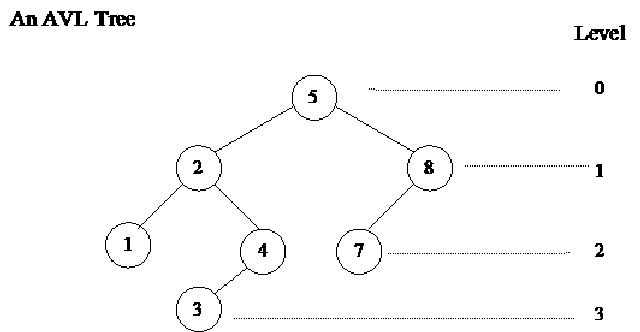
We can calculate the height of a subtree by counting its levels from the bottom. At some node, we calculate the height of its left subtree and right subtree and get the difference between them. Let’s understand this with the help of following fig.
This is an AVL tree. The root of the tree is 5. At next level, we have 2 and 8, followed by 1, 4 and 7 at next level where 1, 4 are left and right subtrees of node 2 and 7 is the left subtree of node 8. At the level three, we have 3. We have shown the levels in the figure at the right side. The root is at level 0, followed by the levels 1, 2 and 3. Now see the height of the left subtree of 5. It is 3. Similarly the height of the right subtree is 2. Now we have to calculate the difference of the height of left subtree and right subtree of 5. The height of left subtree of 5 is 3 and height of right subtree of 5 is 2. So the difference is 1. Similarly, we can have a tree in which right subtree is deeper than left subtree. The condition in the AVL tree is that at any node the height of left subtree can be one more or one less than the height of right subtree. These heights, of course, can be equal. The difference of heights can not be more than 1. This difference can be -1 if we subtract the height of left subtree from right subtree where the height of left subtree is one less than the height of right subtree. Remember that this condition is not at the root. It should satisfy at any level at any node. Let’s analyze the height of left subtree and right subtree of node 2. This should be -1, 0 or 1. The height of left subtree of node 2 is 1 while that of right subtree of the node 2 is 2. Therefore the absolute difference between them is 1. Similarly at node 8, the height of left subtree is 1 and right subtree does not exist so its height is zero. Therefore the difference is 1. At leaves, the height is zero, as there is no left or right subtree. In the above figure, the balanced condition is satisfactory at every level and node. Such trees have a special structure.
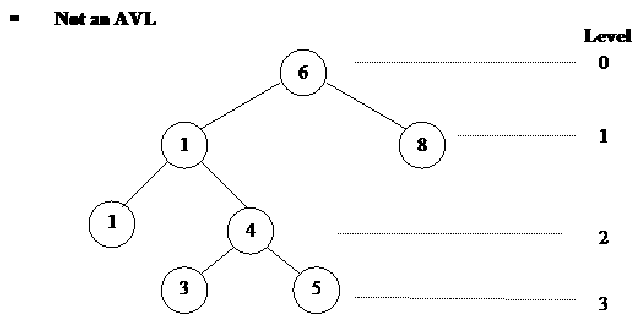
Let’s see another example. Here is the diagram of the tree.
The height of the left subtree of node 6 is three whereas the height of the right subtree is one. Therefore the difference is 2. The balanced condition is not satisfactory. Therefore, it is not an AVL tree.
Let’s give this condition a formal shape that will become a guiding principle for us while creating a tree. We will try to satisfy this condition during the insertion of a node in the tree or a deletion of a node from the tree. We will also see later how we can enforce this condition satisfactorily on our tree. As a result, we will get a tree whose structure will not be like a singly linked list.
The definition of height of a tree is:
The height of a tree is the longest path from the root to the leaf. This can also be calculated as the maximum level of the tree. If we have to calculate the height of some node, we should start counting the levels from that node.
The balance of a node is defined as:
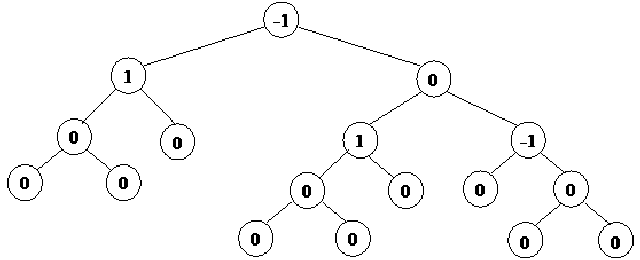
Here, for example, is a balanced tree whose each node has an indicated balance of 1, 0, or –1.
In this example, we have shown the balance of each node instead of the data item. In the root node, there is the value -1. With this information, you know that the height of the right subtree at this node is one greater than that of the left subtree. In the left subtree of the root, we have node with value 1. You can understand from this example that the height of the right subtree at this node is one less than the height of the left subtree. In this tree, some nodes have balance -1, 0 or 1. You have been thinking that we have to calculate the balance of each node. How can we do that? When we create a tree, there will be a need of some information on the balance factor of each node. With the help of this information, we will try to balance the tree. So after getting this balance factor for each node, we will be able to create a balance tree even with the sorted data. There are other cases, which we will discuss, in the next lecture. In short, a balance tree with any kind of data facilitates the search process.
Explanation
In the year 1962, two Russian scientists, Adelson-Velskii and Landis, proposed the criteria to save the binary search tree (BST) from its degenerate form. This was an effort to propose the development of a balanced search tree by considering the height as a standard. This tree is known as AVL tree. The name AVL is an acronym of the names of these two scientists.
An AVL tree is identical to a BST, barring one difference i.e. the height of the left and right sub-trees can differ by at most 1. Moreover, the height of an empty tree is defined to be (–1).
Keeping in mind the idea of the level of a tree, we can understand that if the root of a tree is at level zero, its two children (subtrees) i.e. nodes will be at level 1. At level 2, there will be 4 nodes in case of a complete binary tree. Similarly at level 3, the number of nodes will be 8 and so on. As discussed earlier, in a complete binary tree, the number of nodes at any level k will be 2k. We have also seen the level order traversal of a tree. The term height is identical to the level of a tree. Following is the figure of a tree in which level/height of nodes is shown.
![clip_image001[5] clip_image001[5]](http://lh4.ggpht.com/-8aAP8-M58Ko/UKkdk8QTnzI/AAAAAAAABhA/7jn4Ise7Wvo/clip_image0015_thumb1.gif?imgmax=800)
Here in the figure, the root node i.e. 5 is at the height zero. The next two nodes 2 and 8 are at height (or level) 1. Then the nodes 1, 4 and 7 are at height 2 i.e. two levels below the root. At the last, the single node 3 is at level (height) 3. Looking at the figure, we can say that the maximum height of the tree is 3. AVL states that a tree should be formed in such a form that the difference of the heights (maximum no of levels i.e. depth) of left and right sub-trees of a node should not be greater than 1. The difference between the height of left subtree and height of right subtree is called the balance of the node. In an AVL tree, the balance (also called balance factor) of a node will be 1,0 or –1 depending on whether the height of its left subtree is greater than, equal to or less than the height of its right subtree.
Now consider the tree in the figure 20.1. Its root node is 5. Now go to its left subtree and find the deepest node in this subtree. We see that node 3 is at the deepest level. The level of this deepest node is 3, which means the height of this left subtree is 3. Now from node 5, go to its right subtree and find the deepest level of a node. The node 7 is the deepest node in this right subtree and its level is 2. This means that the height of right subtree is 2. Thus the difference of height of left subtree (i.e. 3) and height of right subtree (i.e. 2) is 1. So according to the AVL definition, this tree is balanced one. But we know that the AVL definition does not apply only to the root node of the tree. Every node (non-leaf or leaf) should fulfill this definition. This means that the balance of every node should be 1, 0 or –1. Otherwise, it will not be an AVL tree.
Now consider the node 2 and apply the definition on it. Let’s see the result. The left subtree of node 2 has the node 1 at deepest level i.e. level 2. The node 2, itself, is at level 1, so the height of the left subtree of node 2 is 2-1 i.e. 1. Now look at the right subtree of node 2. The deepest level of this right subtree is 3 where the node 3 exists. The height of this right subtree of node 2 will be 3 –1 = 2 as the level of node 2 is 1. Now the difference of the height of left subtree (i.e. 1) and height of the right subtree (i.e. 2) is –1. We subtract the height of left subtree from the height of the right subtree and see that node 2 also fulfills the AVL definition. Similarly we can see that all other nodes of the tree (figure 20.1) fulfill the AVL definition. This means that the balance of each node is 1, 0 or –1. Thus it is an AVL tree, also called the balanced tree. The following figure shows the tree with the balance of each node.
Let’s consider a tree where the condition of an AVL tree is not being fulfilled. The following figure shows such a tree in which the balance of a node (that is root node 6) is greater than 1. In this case, we see that the left subtree of node 6 has height 3 as its deepest nodes 3 and 5 are at level 3. Whereas the height of its right subtree is 1 as the deepest node of right subtree is 8 i.e. level 1. Thus the difference of heights (i.e. balance) is 2. But according to AVL definition, the balance should be1, 0 or –1. As shown in the figure, this node 6 is only the node that violates the AVL definition (as its balance is other than 1, 0 and -1). The other nodes fulfill the AVL definition. We know that to be an AVL tree, each node of the tree should fulfill the definition. Here in this tree, the node 6 violates this definition so this is not an AVL tree.
From the above discussion, we encounter two terms i.e. height and balance which can be defined as under.
Height
The height of a binary tree is the maximum level of its leaves. This is the same definition as of depth of a tree.
Balance
The balance of a node in a binary search tree is defined as the height of its left subtree minus height of its right subtree. In other words, at a particular node, the difference in heights of its left and right subtree gives the balance of the node.
The following figure shows a balanced tree. In this figure the balance of each node is shown along with. We can see that each node has a balance 1, 0 or –1.
![clip_image004[5] clip_image004[5]](http://lh5.ggpht.com/-ewefWHP0E1E/UKkdwZuCjiI/AAAAAAAABhw/m5T3V_jrh2g/clip_image0045_thumb1.gif?imgmax=800)
Here in the figure, we see that the balance of the root (i.e. node 6) is –1. We can find out this balance. The deepest level of the left subtree is 3 where the nodes 1 and 3 are located. Thus the height of left subtree is 3. In the right subtree, we see some leaf nodes at level 3 while some are found at level 4. But we know that the height of the tree is the maximum level. So 4 is the height of the right subtree. Now we know that the balance of the root node will be the result of height of left subtree minus the height of right subtree. Thus the balance of the root node is 3 – 4 = -1. Similarly we can confirm the balance of other nodes. The confirmation of balance of the other nodes of the tree can be done. You should do it as an exercise. The process of height computation should be understood as it is used for the insertion and deletion of nodes in an AVL tree. We may come across a situation, when the tree does not remain balanced due to insertion or deletion. For making it a balanced one, we have to carry out the height computations.
While dealing with AVL trees, we have to keep the information of balance factor of the nodes along with the data of nodes. Similarly, a programmer has to have additional information (i.e. balance) of the nodes while writing code for AVL tree.
Insertion of Node in an AVL Tree
Now let’s see the process of insertion in an AVL tree. We have to take care that the tree should remain AVL tree after the insertion of new node(s) in it. We will now see how an AVL tree is affected by the insertion of nodes.
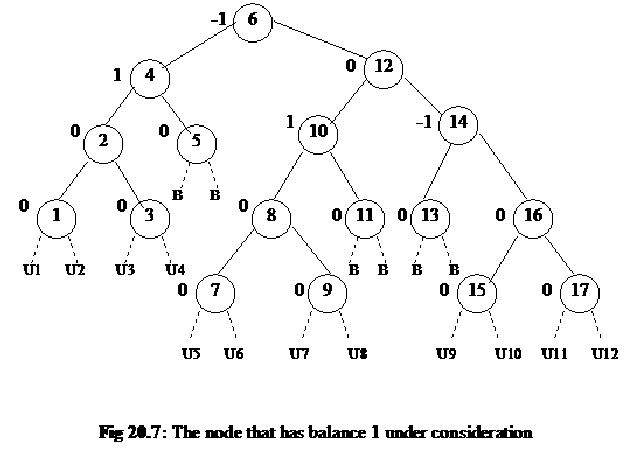
We have discussed the process of inserting a new node in a binary search tree in previous lectures. To insert a node in a BST, we compare its data with the root node. If the new data item is less than the root node item in a particular order, this data item will hold its place in the left subtree of the root. Now we compare the new data item with the root of this left subtree and decide its place. Thus at last, the new data item becomes a leaf node at a proper place. After inserting the new data item, if we traverse the tree with the inorder traversal, then that data item will become at its appropriate position in the data items. To further understand the insertion process, let’s consider the tree of figure 20.4. The following figure (Fig 20.5) shows the same tree with the difference that each node shows the balance along with the data item. We know that a new node will be inserted as a leaf node. This will be inserted where the facility of adding a node is available. In the figure, we have indicated the positions where a new node can be added. We have used two labels B and U for different positions where a node can be added. The label B indicates that if we add a node at this position, the tree will remain balanced tree. On the other hand, the addition of a node at the position labeled as U1, U2 ….U12, the tree will become unbalanced. That means that at some node the difference of heights of left and right subtree will become greater than 1.
By looking at the labels B, U1, U2 …….U12, we conclude some conditions that will be implemented while writing the code for insert method of a balanced tree.
We may conclude that the tree becomes unbalanced only if the newly inserted node
(in the figure 20.5 these positions are U1, U2 …..U8)
(in the tree in fig 20.5 these positions are U9, U10, U11 and U12)
The above conditions are obvious. The balance 1 of a node indicates that the height of its left subtree is 1 more than the height of its right subtree. Now if we add a node to this left subtree, it will increase the level of the tree by 1. Thus the difference of heights will become 2. It violates the AVL rule, making the tree unbalanced.
Similarly the balance –1 of a node indicates that the right subtree of this node is one level deep than the left subtree of the node. Now if the new node is added in the right subtree, this right subtree will become deeper. Its depth/height will increase as a new node is added at a new level that will increase the level of the tree and the height. Thus the balance of the node, that previously has a balance –1, will become –2.
The following figure (Fig 20.6) depicts this rule. In this figure, we have associated the new positions with their grand parent. The figure shows that U1, U2, U3 and U4 are the left descendents of the node that has a balance 1. So according to the condition, the insertion of new node at these positions will unbalance the tree. Similarly the positions U5, U6, U7 and U8 are the left descendents of the node that has a balance 1. Moreover we see that the positions U9, U10, U11 and U12 are the right descendents of the node that has balance –1. So according to the second condition as stated earlier, the insertion of a new node at these positions would unbalance the tree.
Now let’s discuss what should we do when the insertion of a node makes the tree unbalanced. For this purpose, consider the node that has a balance 1 in the previous tree. This is the root of the left subtree of the previous tree. This tree is shown as shaded in the following figure.
We will now focus our discussion on this left subtree of node having balance 1 before applying it to other nodes. Look at the following figure (Fig 20.8). Here we are talking about the tree that has a node with balance 1 as the root. We did not mention the other part of the tree. We indicate the root node of this left subtree with label A. It has balance 1. The label B mentions the first node of its left subtree. Here we did not mention other nodes individually. Rather, we show a triangle that depicts all the nodes in subtrees. The triangle T3 encloses the right subtree of the node A. We are not concerned about the number of nodes in it. The triangles T1 and T2 mention the left and right subtree of the B node respectively. The balance of node B is 0 that describes that its left and right subtrees are at same height. This is also shown in the figure. Similarly we see that the balance of node A is 1 i.e. its left subtree is one level deep than its right subtree. The dotted lines in the figure show that the difference of depth/height of left and right subtree of node A is 1 and that is the balance of node A.
Now considering the notations of figure 20.8, let’s insert a new node in this tree and observe the effect of this insertion in the tree. The new node can be inserted in the tree T1, T2 or T3. We suppose that the new node goes to the tree T1. We know that this new node will not replace any node in the tree. Rather, it will be added as a leaf node at the next level in this tree (T1). The following figure (fig 20.9) shows this phenomenon.
Due to the increase of level in T1, its difference with the right subtree of node A (i.e. T3) will become 2. This is shown with the help of dotted line in the above figure. This difference will affect the balances of node A and B. Now the balance of node A becomes 2 while balance of node B becomes 1. These new balances are also shown in the figure. Now due to the balance of node A (that is 2), the AVL condition has been violated. This condition states that in an AVL tree the balance of a node cannot be other than 1, 0 or –1. Thus the tree in fig 20.9 is not a balanced (AVL) tree.
Now the question arises what a programmer should do in case of violation of AVL condition .In case of a binary search tree, we insert the data in a particular order. So that at any time if we traverse the tree with inorder traversal, only sorted data could be obtained. The order of the data depends on its nature. For example, if the data is numbers, these may be in ascending order. If we are storing letters, then A is less than B and B is less than C. Thus the letters are generally in the order A, B, C ……. This order of letters is called lexographic order. Our dictionaries and lists of names follow this order.
If we want that the inorder traversal of the tree should give us the sorted data, it will not be necessary that the nodes of these data items in the tree should be at particular positions. While building a tree, two things should be kept in mind. Firstly, the tree should be a binary tree. Secondly, its inorder traversal should give the data in a sorted order. Adelson-Velskii and Landis considered these two points
. They said that if we see that after insertion, the tree is going to be unbalanced. Then the things should be reorganized in such a way that the balance of nodes should fulfill the AVL condition. But the inorder traversal should remain the same.
Now let’s see the example of tree in figure 20.9 and look what we should do to balance the tree in such a way that the inorder traversal of the tree remains the same. We have seen in figure 20.9 that the new node is inserted in the tree T1 as a new leaf node. Thus T1has been modified and its level is increased by 1. Now due to this, the difference of T1 and T3 is 2. This difference is the balance of node A as T1 and T3 are its left and right subtrees respectively. The inorder traversal of this tree gives us the result as given below.
T1 B T2 A T3
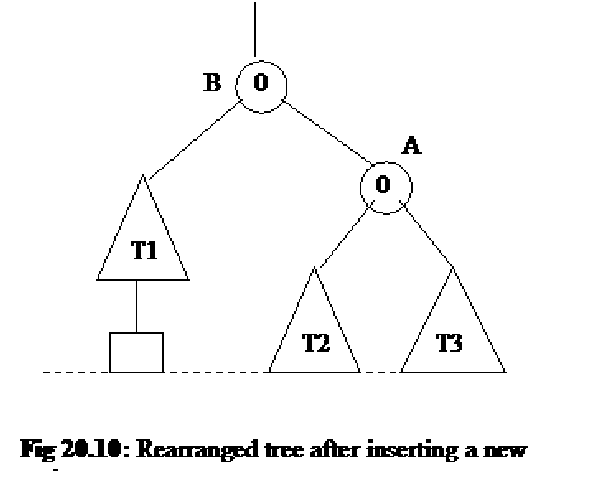
Now we rearrange the tree and it is shown in the following figure i.e. Fig 20.10.
By observing the tree in the above figure we notice at first that node A is no longer the root of the tree. Now Node B is the root. Secondly, we see that the tree T2 that was the right subtree of B has become the left subtree of A. However, tree T3 is still the right subtree of A. The node A has become the right subtree of B. This tree is balanced with respect to node A and B. The balance of A is 0 as T2 and T3 are at the same level. The level of T1 has increased due to the insertion of new node. It is now at the same level as that of T2 and T3. Thus the balance of B is also 0. The important thing in this modified tree is that the inorder traversal of it is the same as in the previous tree (fig 10.9) and is
T1 B T2 A T3
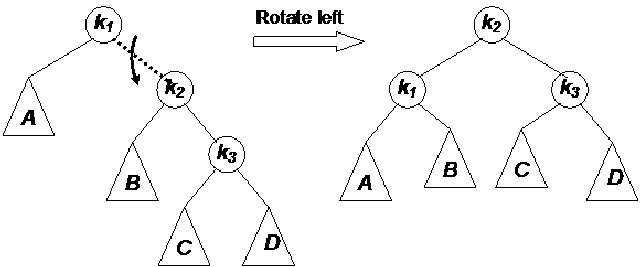
We see that the above two trees give us data items in the same order by inorder traversal. So it is not necessary that data items in a tree should be in a particular node at a particular position. This process of tree modification is called rotation.
Example (AVL Tree Building)
Let’s build an AVL tree as an example. We will insert the numbers and take care of the balance of nodes after each insertion. While inserting a node, if the balance of a node becomes greater than 1 (that means tree becomes unbalance), we will rearrange the tree so that it should become balanced again. Let’s see this process.
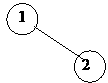
Assume that we have insert routine (we will write its code later) that takes a data item as an argument and inserts it as a new node in the tree. Now for the first node, let’s say we call insert (1). So there is one node in the tree i.e. 1. Next, we call insert (2). We know that while inserting a new data item in a binary search tree, if the new data item is greater than the existing node, it will go to the right subtree. Otherwise, it will go to the left subtree. In the call to insert method, we are passing 2 to it. This data item i.e. 2 is greater than 1. So it will become the right subtree of 1 as shown below.
As there are only two nodes in the tree, there is no problem of balance yet.
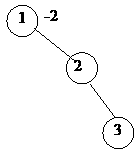
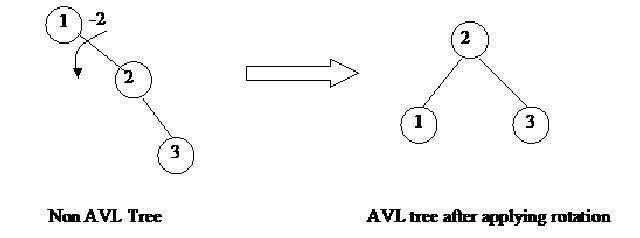
Now insert the number 3 in the tree by calling insert (3). We compare the number 3 with the root i.e.1. This comparison results that 3 will go to the right subtree of 1. In the right subtree of 1 there becomes 2. The comparison of 3 with it results that 3 will go to the right subtree of 2. There is no subtree of 2, so 3 will become the right subtree of 2. This is shown in the following figure.
Let’s see the balance of nodes at this stage. We see that node 1 is at level 0 (as it is the root node). The nodes 2 and 3 are at level 1 and 2 respectively. So with respect to the node 1, the deepest level (height) of its right subtree is 2. As there is no left subtree of node 1 the level of left subtree of 1 is 0. The difference of the heights of left and right subtree of 1 is –2 and that is its balance. So here at node 1, the AVL condition has been violated. We will not insert a new node at this time. First we will do the rotation to make the tree (up to this step) balanced. In the process of inserting nodes, we will do the rotation before inserting next node at the points where the AVL condition is being violated. We have to identify some things for doing rotation. We have to see that on what nodes this rotation will be applied. That means what nodes will be rearranged. Some times, it is obvious that at what nodes the rotation should be done. But there may situations, when the things will not be that clear. We will see these things with the help of some examples.
In the example under consideration, we apply the rotation at nodes1 and 2. We rotate these nodes to the left and thus the node 1 (along with any tree if were associated with it) becomes down and node 2 gets up. The node 3 (and trees associated with it, here is no tree as it is leaf node) goes one level upward. Now 2 is the root node of the tree and 1 and 3 are its left and right subtrees respectively as shown in the following figure.
We see that after the rotation, the tree has become balanced. The figure reflects that the balance of node 1, 2 and 3 is 0. We see that the inorder traversal of the above tree before rotation (tree on left hand side) is 1 2 3. Now if we traverse the tree after rotation (tree on right hand side) by inorder traversal, it is also 1 2 3. With respect to the inorder traversal, both the traversals are same. So we observe that the position of nodes in a tree does not matter as long as the inorder traversal remains the same. We have seen this in the above figure where two different trees give the same inorder traversal. In the same way we can insert more nodes to the tree. After inserting a node we will check the balance of nodes whether it violates the AVL condition. If the tree, after inserting a node, becomes unbalance then we will apply rotation to make it balance. In this way we can build a tree of any number of nodes.
Let’s see the tree’s figures below:
Node containing number 2 became the root node after the rotation of the node having number 1. Note the direction of rotation here.
Let’s insert few more nodes in the tree. We will build an AVL tree and rotate the node when required to fulfill the conditions of an AVL tree.
To insert a node containing number 4,we will, at first, compare the number inside the root node. The current root node is containing number 2. As 4 is greater than 2, it will take the right side of the root. In the right subtree of the root, there is the node containing number 3. As 4 is also greater than 3, it will become the right child of the node containing number 3.
![clip_image006[7] clip_image006[7]](http://lh3.ggpht.com/-yyiG7gFEsR0/UKkebldHF3I/AAAAAAAABkw/xu8ygwGkQ1s/clip_image0067_thumb1.gif?imgmax=800)
Once we insert a node in the tree, it is necessary to check its balance to see whether it is within AVL defined balance. If it is not so, then we have to rotate a node. The balance factor of the node containing number 4 is zero due to the absence of any left or right subtrees. Now, we see the balance factor of the node containing number 3. As it has no left child, but only right subtree, the balance factor is –1. The balance factor of the node containing number 1 is 0. For the node containing number 2, the height of the left subtree is 1 while that of the right subtree is 2. Therefore, the balance factor of the node containing number 2 is 1 – 2 = -1. So every node in the tree in fig. 21.3 has balance factor either 1 or less than that. You must be remembering that the condition for a tree to be an AVL tree, every node’s balance needs not to be zero necessarily. Rather, the tree will be called AVL tree, if the balance factor of each node in a tree is 0, 1 or –1. By the way, if the balance factor of each node inside the tree is 0, it will be a perfectly balanced tree.
![clip_image008[4] clip_image008[4]](http://lh6.ggpht.com/-1_oRPg-UTsY/UKkef5dh1sI/AAAAAAAABlA/zrD0r-0AAHg/clip_image0084_thumb1.gif?imgmax=800)
Next, we insert a node containing number 5 and see the balance factor of each node. The balance factor for the node containing 5 is 0. The balance factor for node containing 4 is –1 and for the node containing 3 is -2. The condition for AVL is not satisfied here for the node containing number 3, as its balance factor is –2. The rotation operation will be performed here as with the help of an arrow as shown in the above Fig 21.4. After rotating the node 3, the new tree will be as under:
![clip_image010[5] clip_image010[5]](http://lh5.ggpht.com/-fUTlyMQKodc/UKkekmVZi7I/AAAAAAAABlQ/7oSzs0VcQ0Q/clip_image0105_thumb1.gif?imgmax=800)
You see in the above figure that the node containing number 4 has become the right child of the node containing number 2. The node with number 3 has been rotated. It has become the left child of the node containing number 4. Now, the balance factor for different nodes containing numbers 5, 3 and 4 is 0. To get the balance factor for the node containing number 2, we see that the height of the left subtree containing number 2 is 1 while height of the right subtree is 2. So the balance factor of the node containing number 2 is –1. We saw that all the nodes in the tree above in Fig 21.5 fulfill the AVL tree condition.
If we traverse the tree Fig 21.5, in inorder tree traversal, we get:
1 2 3 4 5
Similarly, if we traverse the tree in inorder given in Fig 21.4 (the tree before we had rotated the node containing number 3), following will be the output.
1 2 3 4 5
In both the cases above, before and after rotation, we saw that the inorder traversal of trees gives the same result. Also the root (node containing number 2) remained the same.
See the Fig 21.4 above. Considering the inorder traversal, we could arrange the tree in such a manner that node 3 becomes the root of the tree, node 2 as the left child of node 3 and node 1 as the left child of the node 2. The output after traversing the changed tree in inorder will still produce the same result:
1 2 3 4 5
While building an AVL tree, we rotate a node immediately after finding that that the node is going out of balance. This ensures that tree does not become shallow and remains within the defined limit for an AVL tree.
Let’s insert another element 6 in the tree. The figure of the tree becomes:
The newly inserted node 6 becomes the right child of the node 5. Usually, after the insertion of a node, we will find out the node factor for each node and rotate it immediately. This is carried out after finding the difference out of limit. The balance factor for the node 6 is 0, for node 5 is –1 and 0 for node 3. Node 4 has –1 balance factor and node 1 has 0. Finally, we check the balance factor of the root node, node 2, the left subtree’s height is 1 and the right subtree’s height is 3. Therefore, the balance factor for node 2 is –2, which necessitates the rotation of the root node 2. Have a look on the following figure to see how we have rotated the node 2.
Now the node 4 has become the root of the tree. Node 2, which was the root node, has become the left child of node 4. Nodes 5 and 6 are still on their earlier places while remaining the right child and sub-child of node 4 respectively. However, the node 3, which was left child of node 4, has become the right child of node 2.
Now, let’s see the inorder traversal of this tree:
1 2 3 4 5 6
You are required to practice this inorder traversal. It is very important and the basic point of performing the rotation operation is to preserve the inorder traversal of the tree. There is another point to note here that in Binary Search Tree (BST), the root node remains the same (the node that is inserted first). But in an AVL tree, the root node keeps on changing.
In Fig 21.6: we had to traverse three links (node 2 to node 4 and then node 5) to reach the node 6. While after rotation, (in Fig 21.7), we have to traverse the two links (node 4 and 5) to reach the node 6. You can prove it mathematically that inside an AVL tree built of n items; you can search up to 1.44log2n levels to find a node inside. After this maximum number of links traversal, a programmer will have success or failure, as 1.44log2n is the maximum height of the AVL tree. Consider the BST case, where we had constructed a linked list. If we want to build a BST of these six numbers, a linked list structure is formed. In order to reach the node 6, we will have to traverse five links. In case of AVL tree, we had to traverse two links only.
Let’s add few more items in the AVL tree and see the rotations performed to maintain AVL characteristics of the tree.
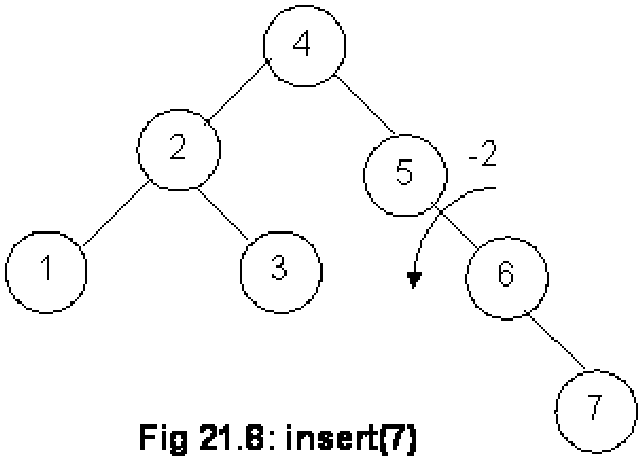
Node 7 is inserted as the right child of node 6. We start to see the balance factors of the nodes. The balance factors for node 7, 6 are 0 and –1 respectively. As the balance factor for node 5 is –2, the rotation will be performed on this node. After rotation, we get the tree as shown in the following figure.
After the rotation, node 5 has become the left child of node 6. We can see in the Fig 21.9 that the tree has become the perfect binary tree. While writing our program, we will have to compute the balance factors of each node to know that the tree is a perfectly balanced binary tree. We find that balance factor for all nodes 7, 5, 3, 1, 6, 2 and 4 is 0. Therefore, we know that the tree is a perfect balanced tree. Let’ see the inorder traversal output here:
1 2 3 4 5 6 7
It is still in the same sequence and the number 7 has been added at the end.
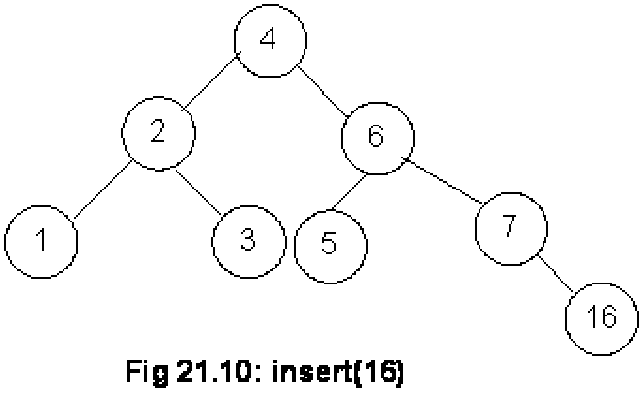
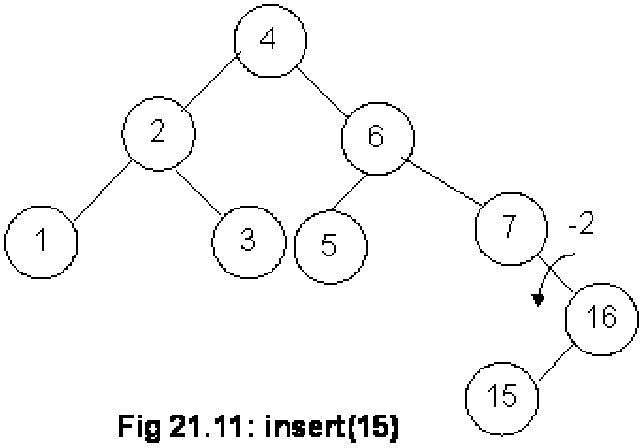
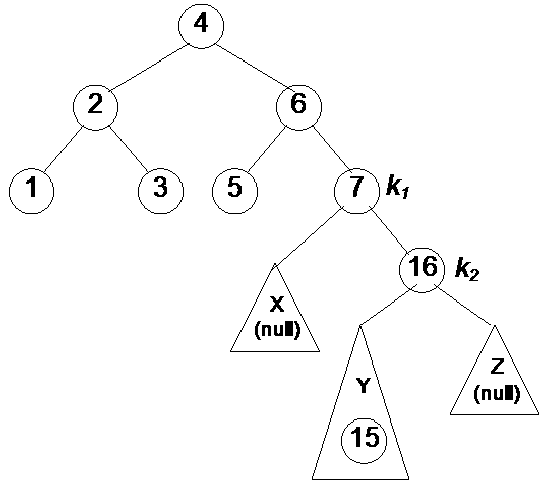
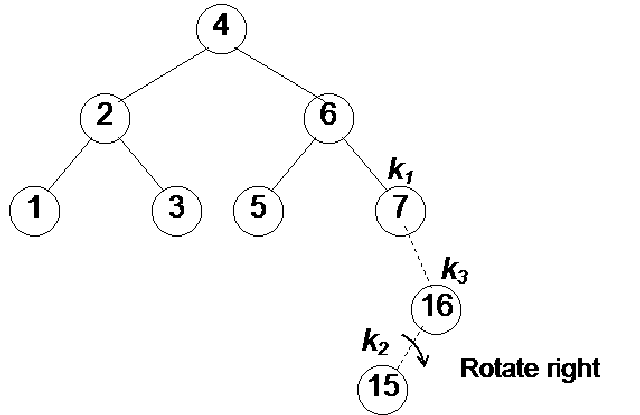
We have inserted a new node 16 in the tree as shown in the above Fig 21.10. This node has been added as the right child of the node 7. Now, let’s compute the balance factors for the nodes. The balance factor for nodes 16, 7, 5, 3, 1, 6, 2 and 4 is either 0 or –1. So this fulfills the condition of a tree to be an AVL. Let’s insert another node containing number 15 in this tree. The tree becomes as given in the figure below:
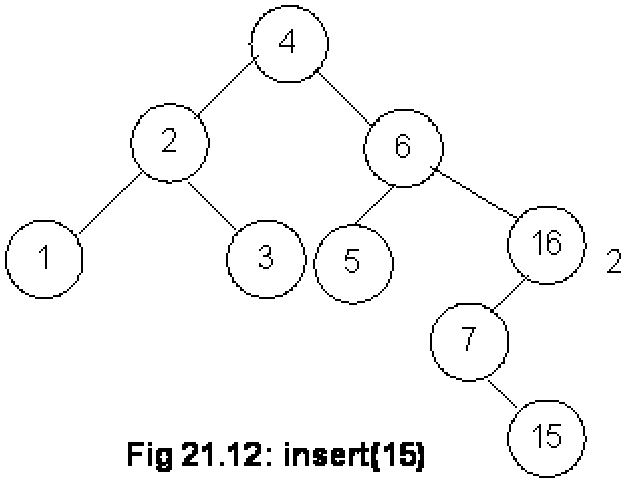
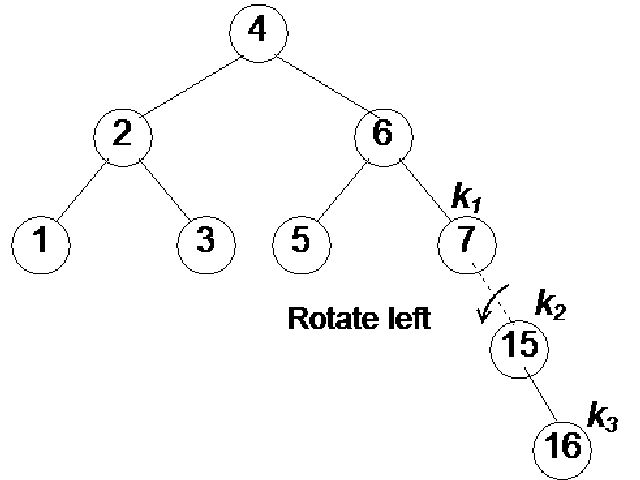
Next step is to find out the balance factor of each node. The factors for nodes 5 and 16 are 0 and 1 respectively. This is within limits of an AVL tree but the balance factor for node 7 is –2. As this is out of the limits of AVL, we will perform the rotation operation here. In the above diagram, you see the direction of rotation. After rotation, we have the following tree:
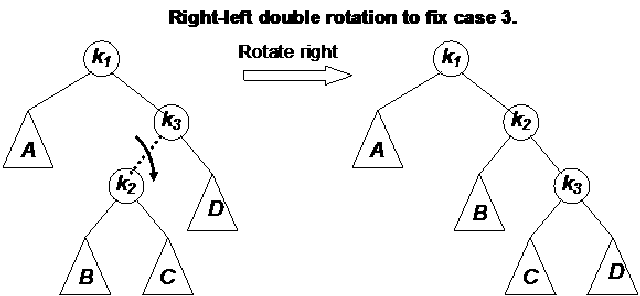
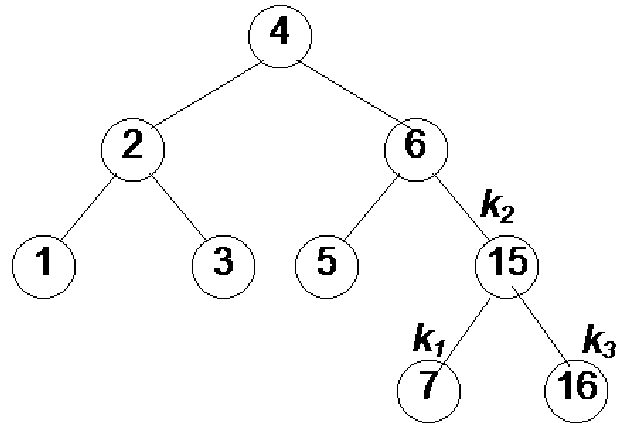
Node 7 has become the left child of node 16 while node 15 has attained the form of the right child of node 7. Now the balance factors for node 15, 7 and 16 are 0, -1 and 2 respectively. Note that the single rotation above when we rotated node 7 is not enough as our tree is still not an AVL one. This is a complex case that we had not encountered before in this example.
Technorati Tags:
ds tutorial,
data structure tutorial,
tree data structure,
trees in data structure,
tree ds,
tree traversal data structure,
tree types,
types of trees,
binary trees,
binary search trees,
bst,
bst data structure,
bst ds,
complete binary search tree,
non tree structure,
linear tree,
avl tree,
avl tree traversal,
avl data structure,
avl ds,
avl tree rotation,
rotation of avl tree,
avl tree tutorial
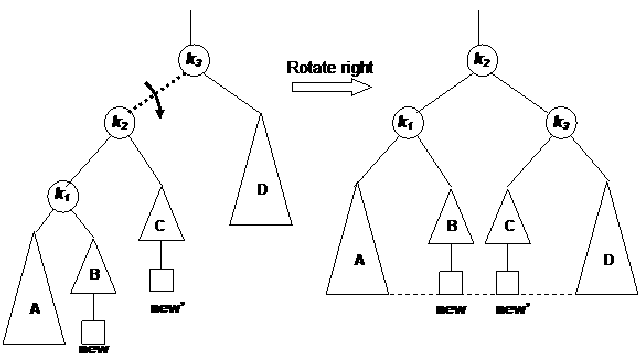
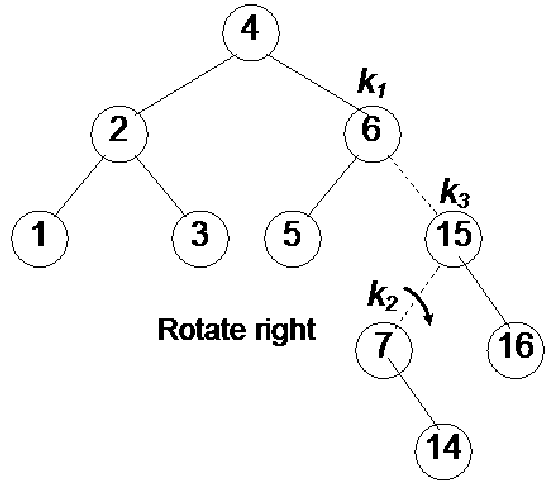
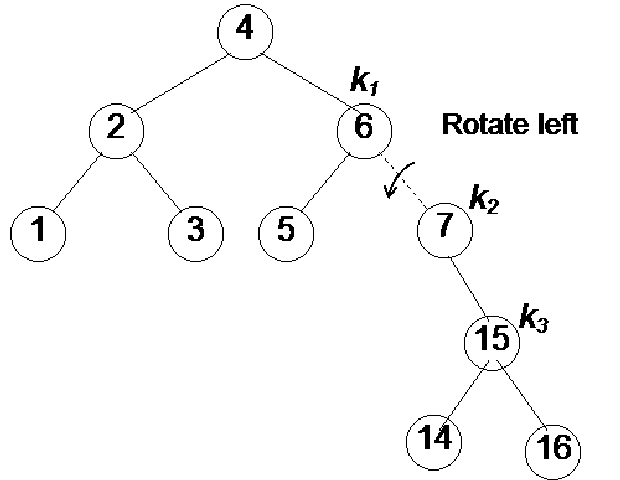
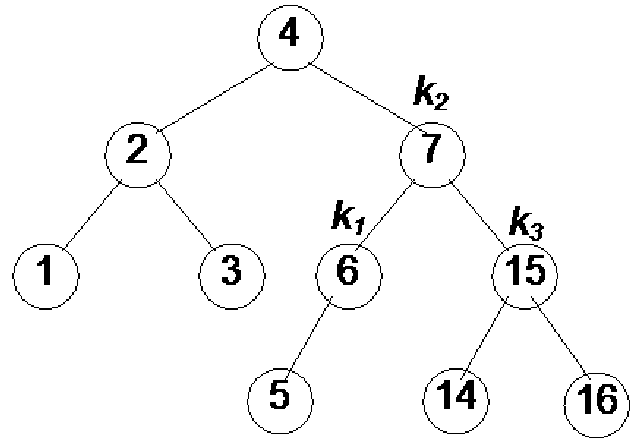
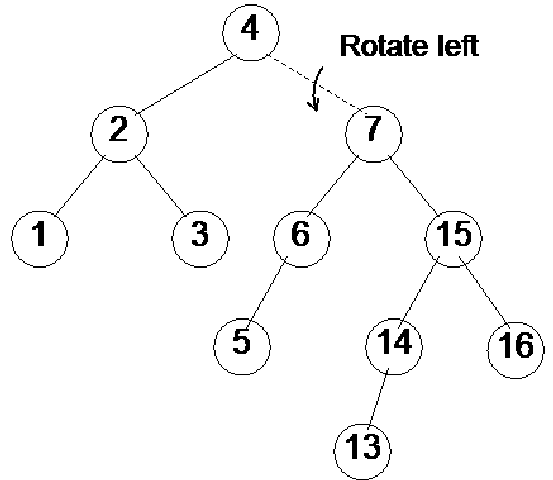
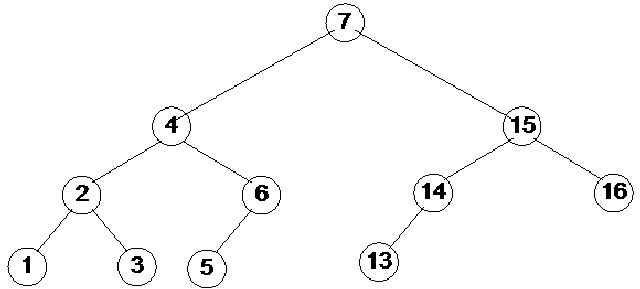
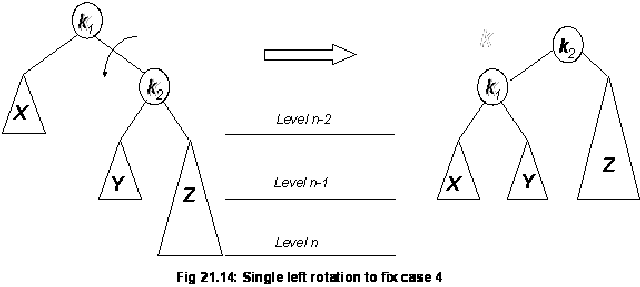 In this figure (Fig 21.14), the new node has been inserted as a child node of Z, that is why it is shown in bigger size covering the next level. Now this is an example of case 4 because the new node is inserted below the right subtree of the right child of the root node (a). One rotation towards should make it balanced within limits of AVL tree. The figure on the right is after rotation the node k1 one time towards left. This time node Y has become the right child node of the node k1.
In this figure (Fig 21.14), the new node has been inserted as a child node of Z, that is why it is shown in bigger size covering the next level. Now this is an example of case 4 because the new node is inserted below the right subtree of the right child of the root node (a). One rotation towards should make it balanced within limits of AVL tree. The figure on the right is after rotation the node k1 one time towards left. This time node Y has become the right child node of the node k1.
![clip_image002[5] clip_image002[5]](http://lh6.ggpht.com/-_oZBR_UgsQw/UKkuRY4XSAI/AAAAAAAABps/5ULLITn-ItI/clip_image0025_thumb1.gif?imgmax=800)
![clip_image004[5] clip_image004[5]](http://lh5.ggpht.com/-dpIhHI6Rtls/UKkuWorphEI/AAAAAAAABqM/X_rB7qoT-u4/clip_image0045_thumb1.gif?imgmax=800)
![clip_image006[5] clip_image006[5]](http://lh4.ggpht.com/-dhXCUeF9pkM/UKkub-IDz_I/AAAAAAAABqo/66r43WN6Y8M/clip_image0065_thumb1.gif?imgmax=800)
![clip_image001[5] clip_image001[5]](http://lh4.ggpht.com/-8aAP8-M58Ko/UKkdk8QTnzI/AAAAAAAABhA/7jn4Ise7Wvo/clip_image0015_thumb1.gif?imgmax=800)
![clip_image002[5] clip_image002[5]](http://lh3.ggpht.com/-WYuyKu82BsY/UKkdoYU4YTI/AAAAAAAABhQ/GzIra6WMAhw/clip_image0025_thumb1.gif?imgmax=800)
![clip_image003[5] clip_image003[5]](http://lh6.ggpht.com/-sNjC6A10M4E/UKkdsQffubI/AAAAAAAABhg/ej08J1zZn1M/clip_image0035_thumb1.gif?imgmax=800)
![clip_image004[5] clip_image004[5]](http://lh5.ggpht.com/-ewefWHP0E1E/UKkdwZuCjiI/AAAAAAAABhw/m5T3V_jrh2g/clip_image0045_thumb1.gif?imgmax=800)
![clip_image005[5] clip_image005[5]](http://lh6.ggpht.com/-uNQQEnut1aE/UKkdzy8hv7I/AAAAAAAABiA/fdJvU_QVPkQ/clip_image0055_thumb1.gif?imgmax=800)
![clip_image006[5] clip_image006[5]](http://lh5.ggpht.com/-1yYbW9ivTDQ/UKkd33w874I/AAAAAAAABiQ/Qt5hYF3WW1U/clip_image0065_thumb1.gif?imgmax=800)
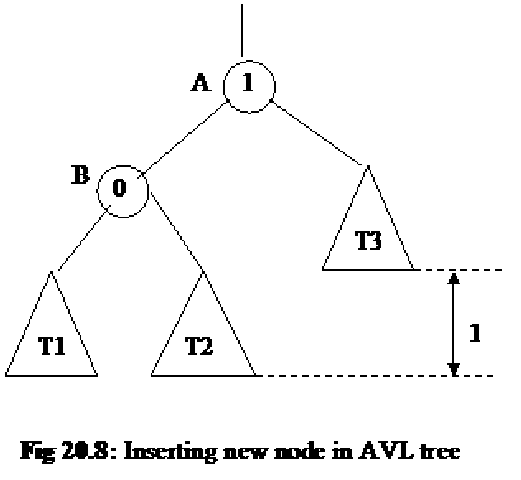
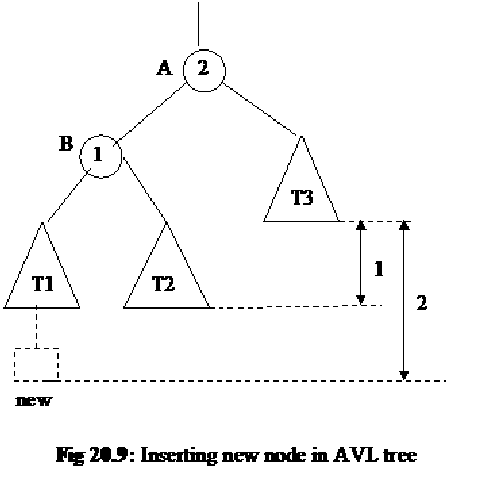
![clip_image002[7] clip_image002[7]](http://lh3.ggpht.com/-_9pCaNNu5h8/UKkeVHZp13I/AAAAAAAABkQ/U-2hGFxlaBY/clip_image0027_thumb1.gif?imgmax=800)
![clip_image004[7] clip_image004[7]](http://lh4.ggpht.com/-nTI_cRdvDjY/UKkeYVU9xJI/AAAAAAAABkg/UQQMhHeuJKc/clip_image0047_thumb1.gif?imgmax=800)
![clip_image006[7] clip_image006[7]](http://lh3.ggpht.com/-yyiG7gFEsR0/UKkebldHF3I/AAAAAAAABkw/xu8ygwGkQ1s/clip_image0067_thumb1.gif?imgmax=800)
![clip_image008[4] clip_image008[4]](http://lh6.ggpht.com/-1_oRPg-UTsY/UKkef5dh1sI/AAAAAAAABlA/zrD0r-0AAHg/clip_image0084_thumb1.gif?imgmax=800)
![clip_image010[5] clip_image010[5]](http://lh5.ggpht.com/-fUTlyMQKodc/UKkekmVZi7I/AAAAAAAABlQ/7oSzs0VcQ0Q/clip_image0105_thumb1.gif?imgmax=800)
![clip_image012[6] clip_image012[6]](http://lh4.ggpht.com/-yOGIYCsHeYk/UKkeoIZWzsI/AAAAAAAABlg/LyzQh50163U/clip_image0126_thumb1.gif?imgmax=800)
![clip_image014[5] clip_image014[5]](http://lh6.ggpht.com/-lXg51iK5zz4/UKkesCXsKTI/AAAAAAAABlw/rx51swREQkI/clip_image0145_thumb1.gif?imgmax=800)