Deleting a Node From Binary Search Tree

 

Until now, we have been discussing about adding data elements in a binary tree but we may also require to delete some data (nodes) from a binary tree. Consider the case where we used binary tree to implement the telephone directory, when a person leaves a city, its telephone number from the directory is deleted.

It is common with many data structures that the hardest operation is deletion. Once we have found the node to be deleted, we need to consider several possibilities.

For case 1, If the node is a leaf, it can be deleted quite easily.

See the tree figure below.

Suppose we want to delete the node containing number 3, as it is a leaf node, it is pretty straight forward. We delete the leaf node containing value 3 and point the right subtree pointer to NULL.

For case 2, if the node has one child, the node can be deleted after its parent adjusts a pointer to bypass the node and connect to inorder successor.

If we want to delete the node containing number 4 then we have to adjust the right subtree pointer in the node containing value 2 to the inorder successor of 4. The important point is that the inorder traversal order has to be maintained after the delete.

The case 3 is bit complicated, when the node to be deleted has both left and right subtrees.

The strategy is to replace the data of this node containing the smallest data of the right subtree and recursively delete that node.

Let’s see this strategy in action. See the tree below:

In this tree, we want to delete the node containing number 2. Let’s do inorder traversal of this tree first. The inorder traversal give us the numbers: 1, 2, 3, 4, 5, 6 and 8.

In order to delete the node containing number 2, firstly we will see its right subtree and find the left most node of it.

The left most node in the right subtree is the node containing number 3. Pay attention to the nodes of the tree where these numbers are present. You will notice that node containing number 3 is not right child node of the node containing number 2 instead it is left child node of the right child node of number 2. Also the left child pointer of node containing number 3 is NULL.

After we have found the left most node in the right subtree of the node containing number 2, we copy the contents of this left most node i.e. 3 to the node to be deleted with number 2.

Next step is to delete the left most node containing value 3. Now being the left most node, there will be no left subtree of it, it might have a right subtree. Therefore, the deletion of this node is the case 2 deletion and the delete operation can be called recursively to delete the node.

Now if we traverse the tree in inorder, we get the numbers as: 1, 3, 4, 5, 6 and 8. Notice that these numbers are still sorted.

Technorati Tags: ds tutorial,data structure tutorial,tree data structure,trees in data structure,tree ds,tree traversal data structure,tree types,types of trees,binary trees,binary search trees,bst,bst data structure,bst ds,complete binary search tree,non tree structure,linear tree,binary search tree,deleting a node from bst,deleting node binary search tree

Binary Search Tree

The advantages of the tree data structure over linked list data structure are many. In a linked list, a programmer has to search the whole list to find out a duplicate of a number to be inserted. It is very tedious job as the number of stored items in a linked list is very large. But in case of tree data structure, we get a dynamic structure in which any number of items as long as memory is available, can be stored. By using tree data structure, the search operation can be carried out very fast. Now we will see how the use of binary tree can help in searching the duplicate number in a very fast manner.

 

Cost of Search

Consider the previous example where we inserted the number 17 in the tree. We executed a while loop in the insert method and carried out a comparison in while loop. If the comparison is true, it will reflect that in this case, the number in the node where the pointer p is pointing is not equal to 17 and also q is not NULL. Then we move p actually q to the left or right side. This means that if the condition of the while loop is true then we go one level down in the tree. Thus we can understand it easily that if there is a tree of 6 levels, the while loop will execute maximum 6 times. We conclude from it that in a given binary tree of depth d, the maximum number of executions of the while loop will be equal to d. The code after the while loop will do the process depending upon the result of the while loop. It will insert the new number or display a message if the number was already there in the tree.

Now suppose we have another method find. This method does not insert a new number in the tree. Rather, it traverses a tree to find if a given number is already present in the tree or not. The tree which the find method traverses was made in such an order that all the numbers less than the number at the root are in the left sub-tree of the root while the right sub-tree of the root contains the numbers greater than the number at the root. Now the find method takes a number x and searches out its duplicate in the given tree. The find method will return true if x is present in the tree. Otherwise, it will return false. This find method does the same process that a part of the insert method performs. The difference is that the insert method checks for a duplicate number before putting a number in the tree whereas the find method only finds a number in the tree. Here in the find method, the while loop is also executed at maximum equal to the number of levels of the tree. We do a comparison at each level of the tree until either x is found or q becomes NULL. The loop terminates in case, the number is found or it executes to its maximum number, i.e. equal to the number of levels of the tree.

In the discussion on binary tree, we talked about the level and number of nodes of a binary tree. It was witnessed that if we have a complete binary tree with n numbers of nodes, the depth d of the tree can be found by the following equation:

d = log₂ (n + 1) – 1

Suppose we have a complete binary tree in which there are 100,000 nodes, then its depth d will be calculated in the following fashion.

d = log₂ (100000 + 1) – 1 = log₂ (100001) – 1= 20

The statement shows that if there are 100,000 unique numbers (nodes) stored in a complete binary tree, the tree will have 20 levels. Now if we want to find a number x in this tree (in other words, the number is not in the tree), we have to make maximum 20 comparisons i.e. one comparison at each level. Now we can understand the benefit of tree as compared to the linked list. If we have a linked list of 100,000 numbers, then there may be 100,000 comparisons (supposing the number is not there) to find a number x in the list.

Thus in a tree, the search is very fast as compared to the linked list. If the tree is complete binary or near-to-complete, searching through 100,000 numbers will require a maximum of 20 comparisons or in general, approximately log₂(n). Whereas in a linked list, the comparisons required could be a maximum of n.

Tree with the linked structure, is not a difficult data structure. We have used it to allocate memory, link and set pointers to it. It is not much difficult process. In a tree, we link the nodes in such a way that it does not remain a linear structure. If instead of 100,000, we have 1 million or 10 million or say, 1 billion numbers and want to build a complete binary tree of these numbers, the depth (number of levels) of the tree will be log₂ of these numbers. The log₂ of these numbers will be a small number, suppose 25, 30 or 40. Thus we see that the number of level does not increase in such a ratio as the number of nodes increase. So we can search a number x in a complete binary tree of 1 billion nodes only in 30-40 comparisons. As the linked list of such a large number grows large, the search of a number in such a case will also get time consuming process. The usage of memory space does not cause any effect in the linked list and tree data structures. We use the memory dynamically in both structures. However, time is a major factor. Suppose one comparison takes one micro second, then one billion seconds are required to find a number from a linked list (we are supposing the worst case of search where traversing of the whole list may be needed). This time will be in hours. On the other hand, in case of building a complete binary tree of these one billion numbers, we have to make 30-40 comparisons (as the levels of the tree will be 30-40), taking only 30-40 microseconds. We can clearly see the difference between hours and microseconds. Thus it is better to prefer the process of building a tree of the data to storing it in a linked list to make the search process faster.

 

Binary Search Tree

While discussing the search procedure, the tree for search was built in a specific order. The order was such that on the addition of a number in the tree, we compare it with a node. If it is less than this, it can be added to the left sub-tree of the node. Otherwise, it will be added on the right sub-tree. This way, the tree built by us has numbers less than the root in the left sub-tree and the numbers greater than the root in the right sub-tree. A binary tree with such a property that items in the left sub-tree are smaller than the root and items in the right sub-tree are larger than the root is called a binary search tree (BST). The searching and sorting operations are very common in computer science. We will be discussing them many times during this course. In most of the cases, we sort the data before a search operation. The building process of a binary search tree is actually a process of storing the data in a sorted form. The BST has many variations, which will be discussed later. The BST and its variations play an important role in searching algorithms. As data in a BST is in an order, it may also be termed as ordered tree.

 

Traversing a Binary Tree

Now let’s discuss the ways to print the numbers present in a BST. In a linked list, the printing of stored values is easy. It is due to the fact that we know wherefrom, a programmer needs to start and where the next element is. Equally is true about printing of the elements in an array. We execute a for loop starting from the first element (i.e. index 0) to the last element of the array. Now let’s see how we can traverse a tree to print (display) the numbers (or any data items) of the tree.

We can explain this process with the help of the following example in which we traverse a binary search tree. Suppose there are three nodes tree with three numbers stored in it as shown below.

Fig 13.1: A three node binary tree

Here we see that the root node has the number 14. The left sub-tree has only one node i.e. number 4. Similarly the right sub-tree consists of a single node with the number 15. If we apply the permutations combinations on these three nodes to print them, there may be the following six possibilities.

1: (4, 14, 15)

2: (14, 4, 15)

3: (15, 4, 14)

4: (4, 15, 14)

5: (14, 15, 4)

6: (15, 14, 4)

Look at these six combinations of printing the nodes of the tree. In the first combination, the order of printing the nodes is 4-14-15. It means that left subtree-root-right subtree. In the second combination the order is root-left subtree-right subtree. In the third combination, the order of printing the nodes is right subtree-root-left subtree. The fourth combination has left subtree-right subtree-root. The fifth combination has the order root-rigth subtree- left subtree. Finally the sixth combination has the order of printing the nodes right subtree-root-left subtree. These six possibilities are for the three nodes only. If we have a tree having a large number of nodes, then there may increase number of permutations for printing the nodes.

Let’s see the general procedure of traversing a binary tree. We know by definition that a binary tree consists of three sets i.e. root, left subtree and right subtree. The following figure depicts a general binary tree.

Fig 13.2: A generic binary tree

In this figure, we label the root node with N. The left subtree in the figure is in a triangle labeled as L. This left subtree may consist of any number of nodes. Similarly the right subtree is enclosed in a triangle having the label R. This triangle of right subtree may contain any number of nodes. Following are the six permutations, which we have made for the three nodes previously. To generalize these permutations, we use N, L and R as abbreviations for root, left subtree and right subtree respectively.

1: (L, N, R)

2: (N, L, R)

3: (R, L, N)

4: (L, R, N)

5: (N, R, L)

6: (R, N, L)

In these permutations, the left and right subtree are not single nodes. These may consist of several nodes. Thus where we see L in the permutations, it means traversing the left subtree. Similarly R means traversing the right subtree. In the previous tree of three nodes, these left and right subtrees are of single nodes. However, they can consist of any number of nodes. We select the following three permutations from the above six. The first of these three is (N, L, R), also called as preorder traversal. The second permutation is (L, N, R) which we called inorder traversal. Finally the third permutation, also termed as postorder traversal is (L, R, N). Now we will discuss these preorder, inorder and postorder traversal in detail besides having a look on their working. We will also see the order in which the numbers in the tree are displayed by these traversing methods.

C++ code

Let’s write the C++ code for it. Following is the code of the preorder method.

void preorder(TreeNode<int>* treeNode) { if( treeNode != NULL ) { cout << *(treeNode->getInfo())<<" "; preorder(treeNode->getLeft()); preorder(treeNode->getRight()); } }

In the arguments, there is a pointer to a TreeNode. We may start from any node and the pointer of the node will be provided as argument to the preorder method. In this method, first of all we check whether the pointer provided is NULL or not. If it is not NULL, we print the information stored in that node with the help of the getInfo() method. Then we call the getLeft() method that returns a pointer of left node, which may be a complete subtree. With the help of this method, we get the root of that subtree. We call the preorder method again passing that pointer. When we return from that, the preorder method is called for the right node. Let’s see what is happening in this method. We are calling the preorder method within the preorder method. This is actually a recursive call. Recursion is supported in C++ and other languages. Recursion means that a function can call itself. We may want to know why we are doing this recursive call. We will see some more examples in this regard and understand the benefits of recursive calls. For the time being, just think that we are provided with a tree with a root pointer. In the preorder, we have to print the value of the root node. Don’t think that you are in the preorder method. Rather keep in mind that you have a preorder function. Suppose you want to print out the left subtree in the preorder way. For this purpose, we will call the preorder function. When we come back, the right subtree will be printed. In the right subtree, we will again call the preorder function that will print the information. Then call the preorder function for the left subtree and after that its right subtree. It will be difficult if you try to do this incursion in the mind. Write the code and execute it. You must be knowing that the definition of the binary tree is recursive. We have a node and left and right subtrees. What is left subtree? It is also a node with a left subtree and right subtree. We have shown you how the left subtree and right subtree are combined to become a tree. The definition of tree is itself recursive. You have already seen the recursive functions. You have seen the factorial example. What is factorial of N? It is N multiplied by N-1 factorial. What is N-1 factorial? N-1 factorial is N-1 multiplied by N-2 factorial. This is the recursive definition. For having an answer, it is good to calculate the factorial of one less number till the time you reach at the number 2. You will see these recursions or recursive relations here and also in mathematic courses. In the course of discrete mathematics, recursion method is used. Here we are talking about the recursive calls. We will now see an example to understand how this recursive call works and how can we traverse the tree using the recursion. One of the benefits of recursion that it prints out the information of all the nodes without caring for the size of the tree. If the tree has one lakh nodes, this simple four lines routine will print all the nodes. When compared with the array printing, we have a simple loop there. In the link list also, we have a small loop that executes till the time we have a next pointer as NULL. For tree, we use recursive calls to print it.

Here is the code of the inorder function.

void inorder(TreeNode<int>* treeNode) { if( treeNode != NULL ) { inorder(treeNode->getLeft()); cout << *(treeNode->getInfo())<<" "; inorder(treeNode->getRight()); } }

The argument is the same as in the preorder i.e. a pointer to the TreeNode. If this node is not NULL, we call getLeft() to get the left node and call the inorder function. We did not print the node first here. In the inorder method, there is no need to print the root tree first of all. We start with the left tree. After completely traversing the complete left tree, we print the value of the node. In the end, we traverse the right subtree in recursion.

Hopefully, you have now a fair knowledge about the postorder mechanism too. Here is the code of the postorder method.

void postorder(TreeNode<int>* treeNode) { if( treeNode != NULL ) { postorder(treeNode->getLeft()); postorder(treeNode->getRight()); cout << *(treeNode->getInfo())<<" "; } }

In the postorder, the input argument is a pointer to the TreeNode. If the node is not NULL, we traverse the left tree first. After that we will traverse the right tree and print the node value from where we started.

As all of these above routines are function so we will call them as:

cout << "inorder: "; preorder( root); cout << "inorder: "; inorder( root ); cout << "postorder: "; postorder( root );

Here the root represents the root node of the tree. The size of the tree does not matter as the complete tree will be printed in preorder, inorder and postorder. Let’s discuss an example to see the working of these routines.

Example

Let’s have a look on the following tree.

3 5 7 9 4 17 16 20 18 15 14

This is the same tree we have been using previously. Here we want to traverse the tree. In the bottom of the figure, the numbers are printed with the help of preorder method. These numbers are as 14 4 3 9 7 5 15 18 16 17 20. Now take these numbers and traverse the tree. In the preorder method, we print the root, followed by traversing of the left subtree and the right subtree respectively. As the value of the root node is 14, so it will be printed first of all. After printing the value of the root node, we call the preorder for the left node which is 4. Forget the node 14 as the root is 4 now. So the value 4 is printed and we call the preorder again with the left sub tree i.e. the node with value 3. Now the root is the node with value 3. We will print its value before going to its left. The left side of node with value 3 is NULL. Preorder will be called if condition is false. In this case, no action will be taken. Now the preorder of the left subtree is finished. As the right subtree of this node is also NULL, so there is no need of any action. Now the left subtree of the node with value 4 is complete. The method preorder will be called for the right subtree of the node with value 4. So we call the preorder with the right node of the node with value 4. Here, the root is the node with value 9 that is printed. We will call its left subtree where the node value is 7. It will be followed by its left subtree i.e. node 5 which will be printed.

In the preorder method, we take the root i.e. 14 in this case. Its value is printed, followed by its left subtree and so on. This activity takes us to the extreme left node. Then we back track and print the right subtrees.

Let’s try to understand the inorder method from the following statement.

When we call the inorder function, the numbers will be printed as 3 4 5 7 9 14 15 16 17 18 20. You might have noted that these numbers are in sorted order. When we build the tree, there was no need of sorting the numbers. But here we have the sorted numbers in the inorder method. While inserting a new node, we compare it with the existing ones and place the new node on the left or right side. So during the process of running the inorder on the binary tree, a programmer gets the numbers sorted. Therefore we have a sorting mechanism. If we are given some number, it will not be difficult to get them sorted. This is a new sorting algorithm for you. It is very simple. Just make BST with these numbers and run the inorder traversal. The numbers obtained from the inorder traversal are sorted.

In the inorder method, we do not print the value of node first. We go to traverse its left subtree. When we come back from the left subtree and print the value of this node. Afterwards, we go to the right subtree. Now consider the above tree of figure 13.4. If we start from number 14, it will not be printed. Then we will go to the left subtree. The left subtree is itself a tree. The number 4 is its root. Now being at the node 4, we again look if there is any left subtree of this node. If it has a left subtree, we will not print 4 and call the inorder method on its left subtree. As there is a left subtree of 4 that consists a single node i.e. 3, we go to that node. Now we call the inorder of node 3 to see if there is a subtree of it. As there is no left subtree of 3, the if statement that checks if the node is not NULL will become false. Here the recursive calls will not be executed. We will come back from the call and print the number 3. Thus the first number that is printed in the inorder traversal is 3. After printing 3, we go to its right subtree that is also NULL. So we come back to node 3. Now as we have traversed the left and right subtrees of 3 which itself is a left subtree of 4, thus we have traversed the left subtree of 4. Now we print the value 4 and go to the right subtree of 4. We come at node 9. Before printing 9 we go to its left subtree that leads us to node 7. In this subtree with root 7, we will not print 7. Now we will go to its left subtree which is node 5. We look for the left subtree of 5 which is NULL. Now we print the value 5. Thus, we have so far printed the numbers 3, 4 and 5. Now we come back to 7. After traversing its left subtree, we print the number 7. The right subtree of 7 is NULL. Thus finally, we have traversed the whole tree whose root is 7. It is a left subtree of 9. Now, we will come back to 9 and print it (as its left subtree has been traversed). The right subtree of 9 is NULL. So there is no need to traverse it. Thus the whole tree having 9 as its root has been traversed. So we come back to the root 4, the right subtree of which is the tree with root 9. Resultantly, the left and right subtree of 4 have been traversed now. Thus we have printed the numbers 3, 4, 5, 7 and 9. Now from here (i.e. node 4) we go to the node 14 whose left subtree has been traversed. Now we print 14 and go to its right subtree. The right subtree of 14 has 15 as the root. From here, we repeat the same process earlier carried out in case of the left subtree of 14. As a result of this process, the numbers 15, 16, 17, 18 and 20 are printed. Thus we get the numbers stored in the tree in a sorted order. And we get the numbers printed as 3, 4, 5, 7, 9, 14, 15, 16, 17, 18, 20. This sorted order is only in the inorder traversal.

When we apply the post order traversal on the same tree, the numbers we get are not in sorted order. The numbers got through postorder traversal are in the following order:

3 5 7 9 4 17 16 20 18 15 14

We see that these are not in a sorted order. In order to delete the node from BST, click here.

Technorati Tags: ds tutorial,data structure tutorial,tree data structure,trees in data structure,tree ds,tree traversal data structure,tree types,types of trees,binary trees,binary search trees,bst,bst data structure,bst ds,complete binary search tree,non tree structure,linear tree,binary search tree

Operations on Binary Tree

 
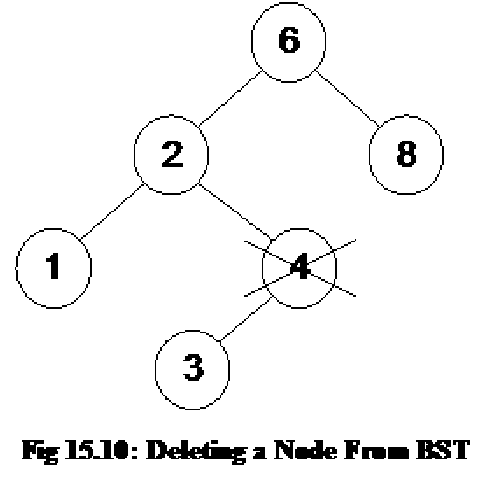
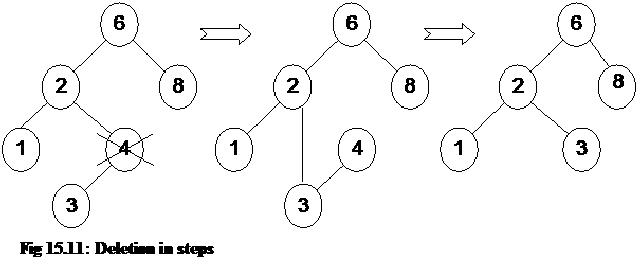
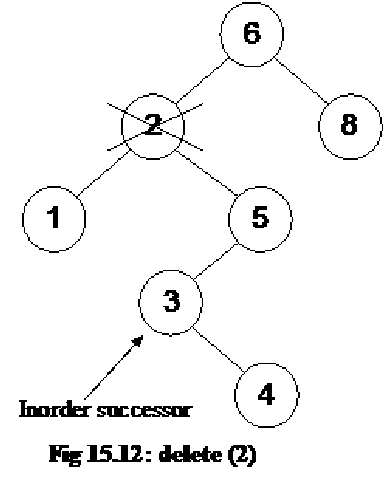
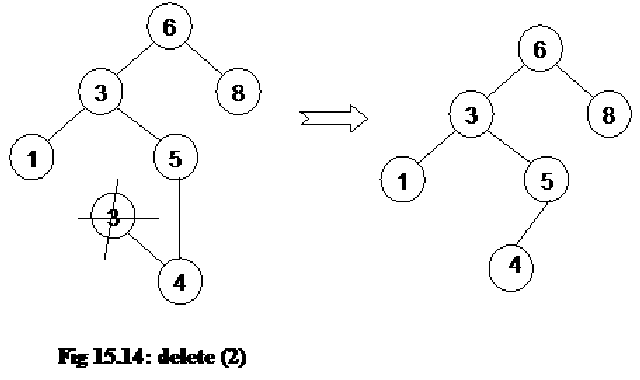
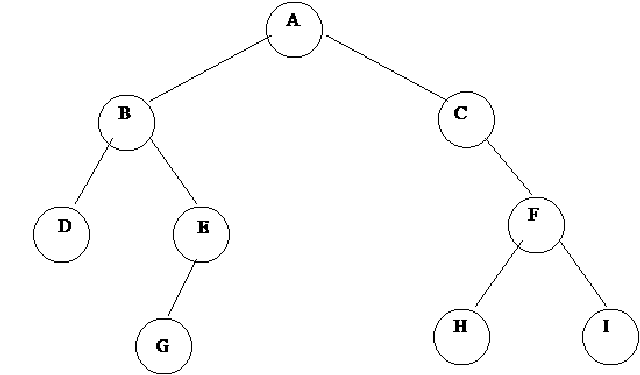
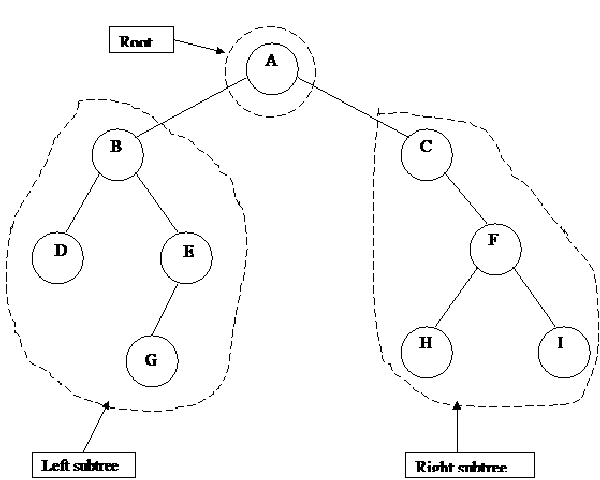
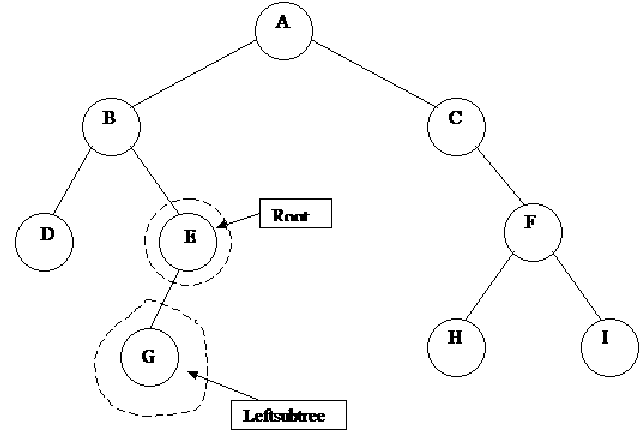
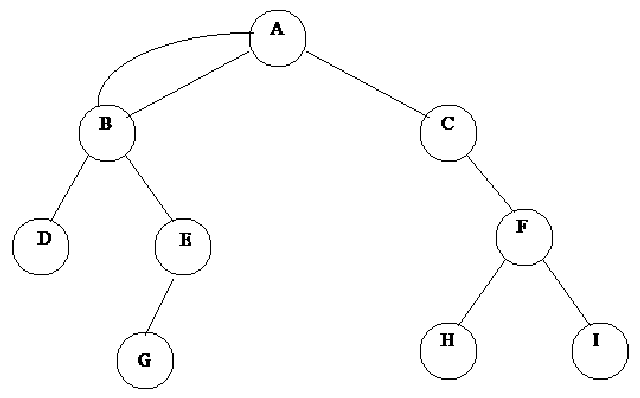
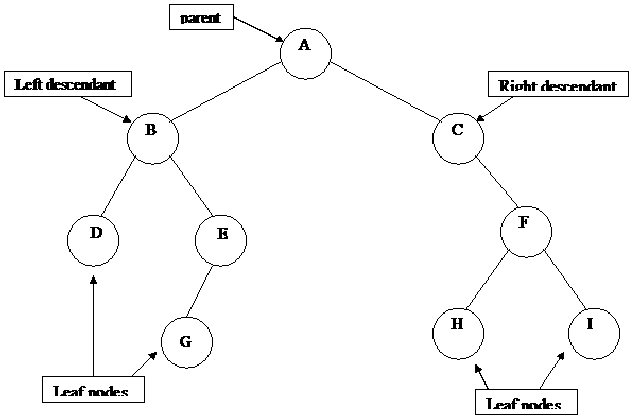
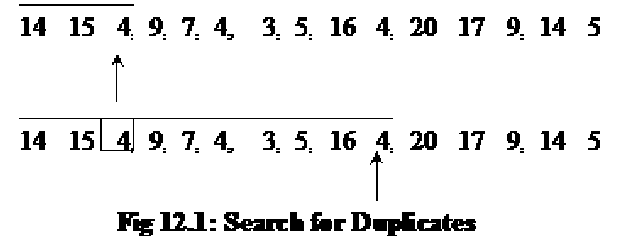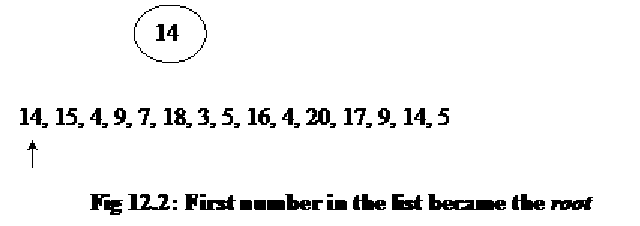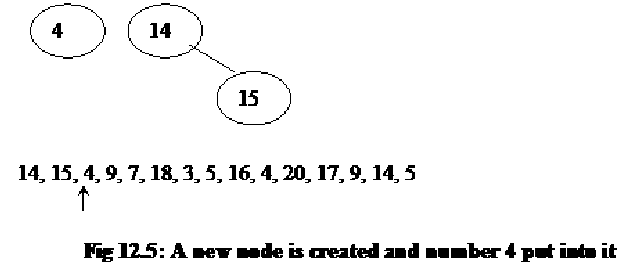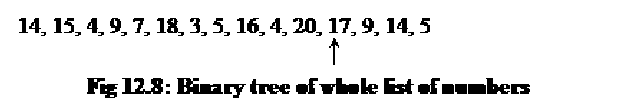We can define different operations on binary trees.
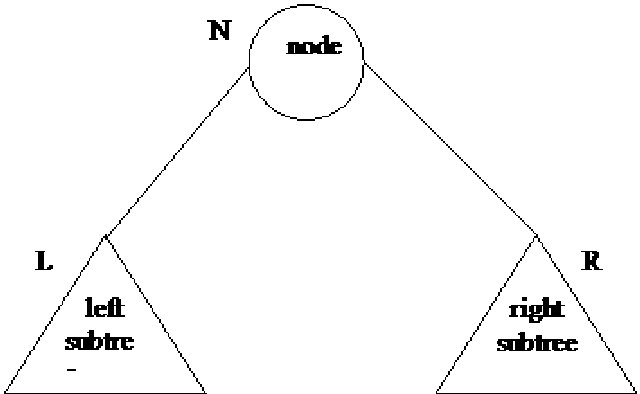
If p is pointing to a node in an existing tree, then

• left(p) returns pointer to the left subtree
• right(p) returns pointer to right subtree
• parent(p) returns the father of p
• brother(p) returns brother of p.

info(p) returns content of the node

Consider a tree has been formed already, following methods will be used to perform different operations on a node of this tree:

Operation	Description
left(p)	Returns a pointer to the left sub-tree
right(p)	Returns a pointer to the right sub-tree
parent(p)	Returns the father node of p
brother(p)	Returns the brother node of p
info(p)	Returns the contents of node p

These methods have already been discussed at the end of the previous lecture, however, few more methods are required to construct a binary tree:

Operation	Description
setLeft(p, x)	Creates the left child node of p and set the value x into it.
setRight(p, x)	Creates the right child node of p, the child node contains the info x.

All these methods are required to build and to retrieve values from a tree.

Applications of Binary Tree

Let’s take few examples to understand how the tree data type is used and what are its benefits. We will also develop some algorithms that may by useful in future while working with this data type.

Binary tree is useful structure when two-way decisions are made at each point. Suppose we want to find all duplicates in a list of the following numbers:

14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5

This list may comprise numbers of any nature. For example, roll numbers, telephone numbers or voter’s list. In addition to the presence of duplicate number, we may also require the frequency of numbers in the list. As it is a small list, so only a cursory view may reveal that there are some duplicate numbers present in this list. Practically, this list can be of very huge size ranging to thousands or millions.

Searching for Duplicates

One way of finding duplicates is to compare each number with all those that precede it. Let’s see it in detail.

Suppose, we are looking for duplicates for the number 4, we will start scanning from the first number 14. While scanning, whenever we find the number 4 inside, we remember the position and increment its frequency counter by 1. This comparison will go on till the end of the list to get the duplicates or fequence of the number 4. You might have understood already that we will have to perform this whole scanning of list every time for each number to find duplicates. This is a long and time consuming process.

So this procedure involves a large number of comparisons, if the list of numbers is large and is growing.

A linked list can handle the growth. But it can be used where a programmer has no idea about the size of the data before hand. The number of comparisons may still be large. The comparisons are not reduced after using linked list as it is a linear data structure. To search a number in a linked list, we have to begin from the start of the list to the end in the linear fashion, traversing each node in it. For optimizing search operation in a list, there is no real benefit of using linked list. On the contrary, the search operation becomes slower even while searching in an array because the linked list is not contiguous like an array and traversing is done in the linked list with the help of pointers.

So, the solution lies in reducing the number of comparisons. The number of comparisons can be drastically reduced with the help of a binary tree. The benefits of linked list are there, also the tree grows dynamically like the linked list.

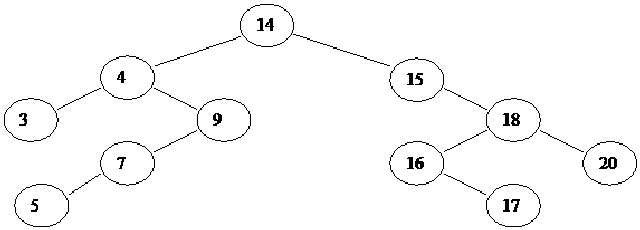
The binary tree is built in a special way. The first number in the list is placed in a node, designated as the root of the binary tree. Initially, both left and right sub-trees of the root are empty. We take the next number and compare it with the number placed in the root. If it is the same, this means the presence of a duplicate. Otherwise, we create a new tree node and put the new number in it. The new node is turned into the left child of the root node if the second number is less than the one in the root. The new node is turned into the right child if the number is greater than the one in the root.

In the above figure, the first number in the list 14 is placed in a node , making it the root of the binary tree. You can see that it is not pointing to any further node. Therefore, its left and right pointers are NULL at this point of tree construction time. Now, let’s see, how do we insert the next element into it.

As a first step to add a new node in the tree, we take the next number 15 in the list and compare it with 14, the number in the root node. As they are different, so a new node is created and the number 15 is set into it.

The next step is to add this node in the tree. We compare 15, the number in the new node with 14, the number in the root node. As number 15 is greater than number 14, therefore, it is placed as right child of the root node.

The next number in the list i.e. 4, is compared with 14, the number in the root node. As the number 4 is less than number 14, so we see if there is a left child of the root node to compare the number 4 with that. At this point of time in the tree, there is no further left child of the root node. Therefore, a new node is created and the number 4 is put into it.

The below figure shows the newly created node.

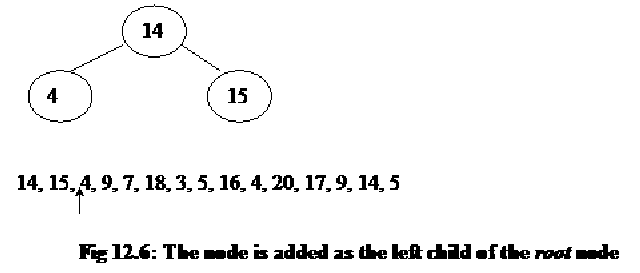
Next, the newly created node is added as the left child of the root node. It is shown in the figure below.

The next number in the list is 9. To add this number in the tree, we will follow the already defined and experimented procedure. We compare this number first with the number in the root node of the tree. This number is found to be smaller than the number in the root node. Therefore, left sub-tree of the root node is sought. The left child of the root node is the one with number 4. On comparison, number 9 is found greater than the number 4. Therefore, we go to the right child of the node with number 4. At the moment, there is no further node to the right of it, necessitating the need of creating a new node. The number 9 is put into it and the new node is added as the right child of the node with number 4. The same is shown in the figure given below.

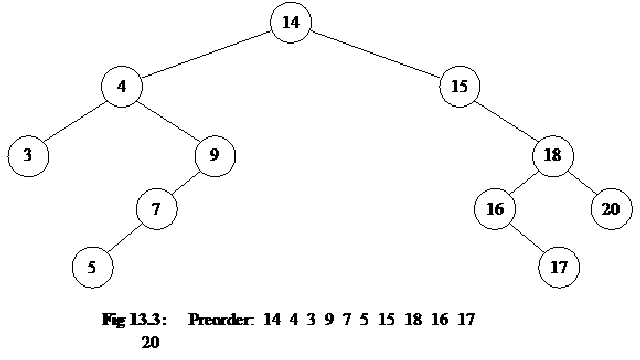
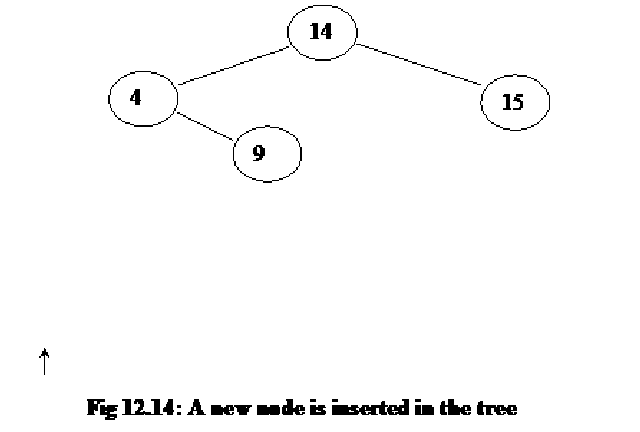
We keep on adding new nodes in the tree in line with the above practiced rule and eventually, we have the tree shown in the below figure.

 

It is pertinent to note that this is a binary tree with two sub-nodes or children of each node. We have not seen the advantage of binary tree, the one we were earlier talking about i.e. it will reduce the number of comparisons. Previously, we found that search operation becomes troublesome and slower as the size of list grows. We will see the benefit of using binary tree over linked list later. Firstly, we will see how the tree is implemented.

 

C++ Implementation of Binary Tree

See the code below for the file treenode.cpp.

/* This file contains the TreeNode class declaration. TreeNode contains the functionality for a binary tree node */ 1. #include <stdlib.h> 2. 3. template <class Object> 4. 5. class TreeNode 6. { 7. public: 8. // constructors 9. TreeNode() 10. { 11. this->object = NULL; 12. this->left = this->right = NULL; 13. }; 14. 15. TreeNode( Object * object ) 16. { 17. this->object = object; 18. this->left = this->right = NULL; 19. }; 20. 21. Object * getInfo() 22. { 23. return this->object; 24. }; 25. 26. void setInfo(Object * object) 27. { 28. this->object = object; 29. }; 30. 31. TreeNode * getLeft() 32. { 33. return left; 34. }; 35. 36. void setLeft(TreeNode * left) 37. { 38. this->left = left; 39. }; 40. 41 TreeNode * getRight() 42. { 43. return right; 44. }; 45. 46. void setRight(TreeNode * right) 47. { 48. this->right = right; 49. }; 50. 51. int isLeaf( ) 52. { 53. if( this->left == NULL && this->right == NULL ) 54. return 1; 55. return 0; 56. }; 57. 58. private: 59. Object * object; 60. TreeNode * left; 61. TreeNode * right; 62. }; // end class TreeNode

For implementation, we normally write a class that becomes a factory for objects of that type. In this case too, we have created a class TreeNode to be used to create nodes of the binary tree. As we want to use this class for different data types, therefore, we will make it a template class, the line 2 is doing the same thing. Inside the class body, we start with the private data members given at the bottom of the class declaration. At line 59, the object is a private data element of Object *, used to store the tree element (value) inside the node of the tree. left is a private data member of type TreeNode*, it is used to store a pointer to the left sub-tree. right is a private data member of type TreeNode*, employed to store a pointer to the right sub-tree.

Now, we go to the top of the class declaration to see the public functions. At line 9, a public parameter-less constructor is declared. The data members have been initialized in the constructor. At line 11, the object data member is initialized to NULL. Similarly left and right data members are initialized to NULL at line 12.

There is another constructor declared at line 15- that takes object value as a parameter to construct a TreeNode object with that object value. While the pointers for right and left sub-trees are pointing to NULL.

At line 21, there is method getInfo(), which returns the object i.e. the element of the TreeNode object.

At line 26, the method setInfo(Object * ) sets the value of the object data member to the value passed to it as the argument.

The method getLeft() returns the pointer to the left sub-tree. Similarly, the getRight() returns the right sub-tree. Note that both of these methods return a pointer to the object of type TreeNode.

The setLeft(TreeNode *) method is used to set the pointer left to left sub-tree. Similarly, setRight(TreeNode *) is used to set the pointer right to right sub-tree. Both of these methods accept a pointer of type TreeNode.

The isLeaf() method at line 51, is to see whether the current node is a leaf node or not. The method returns 1 if it is leaf node. Otherwise, it returns 0.

Using the above TreeNode, nodes for the binary tree can be created and linked up together to form a binary tree. We can write a separate method or a class to carry out the node creation and insertion into tree.

Let’s use this class by writing couple of functions. Below is the code of main program file containing the main() and insert() functions.

1. #include <iostream> 2. #include <stdlib.h> 3. #include "TreeNode.cpp" 4. 5. int main(int argc, char * argv[]) 6. { 7. int x[] = {14,15,4,9,7,18,3,5,16,4,20,17,9,14,5,-1}; 8. TreeNode <int> * root = new TreeNode<int>(); 9. root->setInfo( &x[0] ); 10. for(int i = 1; x[i] > 0; i++ ) 11. { 12. insert( root, &x[i] ); 13. } 14. } 15. 16. void insert (TreeNode <int> * root, int * info) 17. { 18. TreeNode <int> * node = new TreeNode <int> (info); 19. TreeNode <int> * p, * q; 20. p = q = root; 21. while( *info != *(p->getInfo()) && q != NULL ) 22. { 23. p = q; 24. if( *info < *(p->getInfo()) ) 25. q = p->getLeft(); 26. else 27. q = p->getRight(); 28. } 29. 30. if( *info == *( p->getInfo() ) ) 31. { 32. cout << "attempt to insert duplicate: " << *info << endl; 33. delete node; 34. } 35. else if( *info < *(p->getInfo()) ) 36. p->setLeft( node ); 37. else 38. p->setRight( node ); 39. } // end of insert

We have used the same list of numbers for discussion in this lecture. It is given at line 7 in the code. It is the same, only the last number is –1. This is used as delimiter or marker to indicate that the list has finished.

At line 8, we are creating a new TreeNode object i.e. a root node as the name implies. This node will contain an int type element as evident from the syntax.

At line 9, the first number in the list is set into the root node. At line 10, the for loop is started, which is inserting all the elements of the list one by one in the tree with the use of the insert() function. Most of the time, this loop will be reading the input numbers from the users interactively or from a file. It it is Windows application then a form can by used to take input from the user. In this implementation, our objective is to insert numbers in the tree and see the duplicates, so hard coding the numbers within our program will serve the purpose.

The insert() method starts from line 16. It is accepting two parameters. The first parameter is pointer to a TreeNode object, containing a value of int type while second is the info that is an int *.

In the first line of the function, line 18, a new node has been by calling the parameterized constructor of the TreeNode class.

Then at line 19, two pointer variables p and q are declared.

In line 20, we are initializing variables p and q to the root node.

In line 21, the while loop is being started, inside the while loop we are checking the equality of the number inside the node (being pointed to by pointer p) with the number being passed. The control is entered into the loop, if both the numbers are not equal and q is not pointing to NULL. This while loop will be terminated if the numbers in the two nodes are equal or end of a sub-tree is reached.

At line 23 inside the loop, p is assigned the value of q.

At line 24 inside the loop, if the number inside the node is smaller than the number in the node pointed to by the pointer p. Then at line 25, we are getting the left sub-tree address (left) and assigning it to the pointer q.

Otherwise, if this not the case, means the number in the node to be inserted is not smaller than the number in the node pointed to by the pointer p. Then at line 27, the right sub-tree address is retrieved and assigned to pointer q.

At line 30, the comparison is made to see if the both the values are equal (number in the node to be inserted and the number inside the node pointed to by the pointer p). In case they are equal, it displays a message with the number informing that a duplicate number has been found. This also means that the upper while loop was terminated because of equality of the two numbers. In the line 33, the newly created node is deleted afterwards.

At line 35, we are checking if the number in the newly constructed node is less than the number in the node at the end of a sub-tree. If this is so then the newly constructed node is inserted to the left of the tree node. The insertion code is at line 36.

If the number in the newly constructed node is greater than the number in the tree node, the newly constructed node will be inserted to the right of the tree node as shown on line 38. To make it clearer, let’s see the same thing, the insert() method pictorially.

Trace of insert

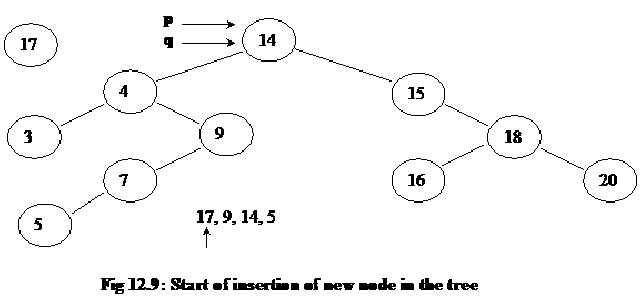
We will take the tree and the figure, we constructed above. At this time, we want to insert some new numbers in the tree as given in the figure below:

p

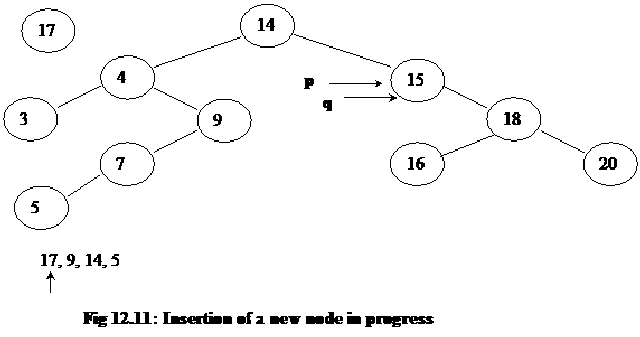
Initially the pointers p and q are pointing to the start (root) of the tree. We want to insert the number 17 in the tree. We compare the number in the root node (14) with number 17. Because number 17 is greater than the number 14, so as we did in the while loop in the function above, we will move toward the right sub-tree. In the next picture below, we can see that the pointer q has moved to the right sub-tree of the root.

After moving the pointer q forward, we make the pointer p point to the same node. We do this operation as the first step inside the while loop. It can be seen at line 23 above. So following will be the latest position of pointers in the tree.

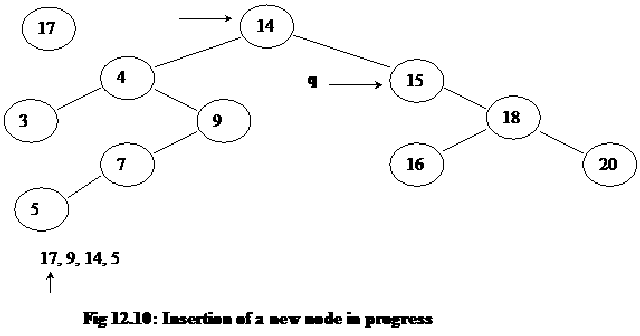
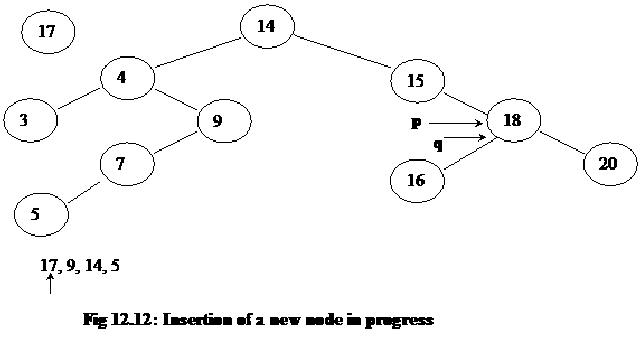
Now, the number 15 in the tree node is compared with new number 17. Therefore, the pointer q is again moved forward to the right child node i.e. the node with number 18. In the next step, we move forward the p pointer also. The following figure depicts the current picture of the tree:

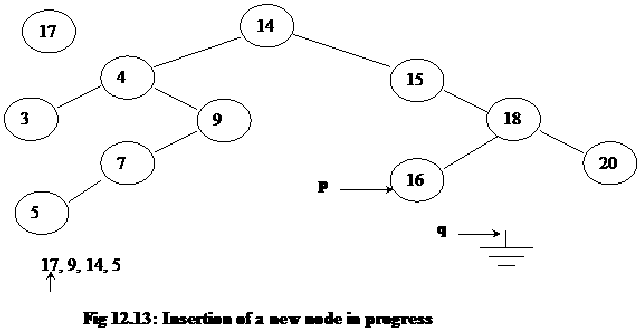
The previous process is repeated again (while loop is the repeating construct) that the number 17 is compared with the number 18. This time the left child node is traversed and q pointer starts pointing the node with number 16 inside. In the next step, p is moved forward to point to the same node as q.

The same comparison process starts again, number 17 is found to be greater than the number 16, therefore, the right child is seek. But we see that the current tree node does not have right child node, so it returns NULL. Following figure depicts it.

Above shown (q is pointing to NULL) is the condition that causes the while loop in the code above to terminate. Later we insert the new node as the right child of the current node.

It is recommended to execute this algorithm manually to insert the remaining numbers in the tree. This will make the understanding more clear. This tree algorithm is going to be used rigorously in the future and complete understanding of it will make the complex future implementations easier to comprehend.

Technorati Tags: ds tutorial,data structure tutorial,tree data structure,trees in data structure,tree ds,tree traversal data structure,tree types,types of trees,binary trees,binary search trees,bst,bst data structure,bst ds,complete binary search tree,non tree structure,linear tree,operation on trees,tree implementation in c++,binary tree implementation in c++

Trees and Binary Tree

This is an important data structure. This data structure is used in many algorithms. The data structures that we have discussed in previous lectures are linear data structures. The linked list and stack are linear data structures. In these structures, the elements are in a line. We put and get elements in and from a stack in linear order. Queue is also a linear data structure as a line is developed in it. There are a number of applications where linear data structures are not appropriate. In such cases, there is need of some non-linear data structure. Some examples will show us that why non-linear data structures are important. Tree is one of the non-linear data structures.

Look at the following figure. This figure (11.1) is showing a genealogy tree of a family.

In this genealogy tree, the node at the top of the tree is Grand Parent i.e. the head of the family. There are three nodes under this one. These are children of Grand Parent. Then there are nodes under these three nodes i.e. the children of these three family members. You may have seen the tree like this of some other family. You can make the tree of your family too. The thing to be noted in this genealogical tree is that it is not a linear structure like linked list, in which we have to tell that who is the father and who is the son. We make it like a tree. We develop the tree top-down, in which the father of the family is on the top with their children downward. We can see the similar tree structure of a company. In the tree of a company, the CEO of the company is on the top, followed downward by the managers and assistant managers. This process goes downward according to the administrative hierarchy of the company. Our tree structure is different from the actual tree in the way that the actual tree grows from down to up. It has root downside and the leaves upside. The data structure tree is opposite to the real tree as it goes upside down. This top-down structure in computer science makes it easy to understand the tree data structure.

There may be situations where the data, in our programs or applications, is not in the linear order. There is a relationship between the data that cannot be captured by a linked list or other linear data structure. Here we need a data structure like tree.

In some applications, the searching in linear data structures is very tedious. Suppose we want to search a name in a telephone directory having 100000 entries. If this directory is in a linked list manner, we will have to traverse the list from the starting position. We have to traverse on average half of the directory if we find a name. We may not find the required name in the entire directory despite traversing the whole list. Thus it would be better to use a data structure so that the search operation does not take a lot of time. Taking into account such applications, we will now talk about a special tree data structure, known as binary tree.

 Binary Tree

The mathematical definition of a binary tree is

“A binary tree is a finite set of elements that is either empty or is partitioned into three disjoint subsets. The first subset contains a single element called the root of the tree. The other two subsets are themselves binary trees called the left and right sub-trees”. Each element of a binary tree is called a node of the tree.

Following figure shows a binary tree.

Fig 11.2: A Binary Tree

There are nine nodes in the above figure of the binary tree. The nine nodes are A, B, C, D, E, F, G, H, and I. The node A is at the top of the tree. There are two lines from the node A to left and right sides towards node B and C respectively. Let’s have a look at the left side of the node A. There are also two lines from node B to left and right, leading to the nodes D and E. Then from node, E there is only one line that is to the left of the node and leads to node G. Similarly there is a line from node C towards the node F on right side of the node C. Then there are two lines from node F that leads to the nodes H and I on left and right side respectively.

Now we analyze this tree according to the mathematical definition of the binary tree. The node A is the root of the tree. And tree structure (i.e. the nodes B, D, E, G and their relation) on the left side of the node A is a sub-tree, called the Left subtree. Similarly the nodes (C, F, H and I) on the right side of the node A comprise the sub-tree termed as Right subtree. Thus we made three parts of the tree. One part contains only one node i.e. A while the second part has all the nodes on left side of A, called as Left subtree. Similarly the third part is the Right subtree, containing the nodes on right side of A. The following figure depicts this scenario.

Fig 11.3: Analysis of a binary tree

The same process of sub classing the tree can be done at the second level. That means the left and right subtrees can also be divided into three parts similarly. Now consider the left subtree of node A. This left subtree is also a tree. The node B is the root of this tree and its left subtree is the node D. There is only one node in this left subtree. The right subtree of the node B consists of two nodes i.e. E and G. The following figure shows the analysis of the tree with root B.

Fig 11.4: Analysis of a binary tree

On going one step down and considering right subtree of node B, we see that E is the root and its left subtree is the single node G. There is no right subtree of node E or we can say that its right subtree is empty. This is shown in the following figure.

Fig 11.5: Analysis of a binary tree

Now the left sub tree of E is the single node G. This node G can be considered as the root node with empty left and right sub trees. The definition of tree is of recursive nature. This is due to the fact that we have seen that which definition has been applied to the tree having node A as root, is applied to its subtrees one level downward. Similarly as long as we go down ward in the tree the same definition is used at each level of the tree. And we see three parts i.e. root, left subtree and right subtree at each level.

Now if we carry out the same process on the right subtree of root node A, the node C will become the root of this right subtree of A. The left subtree of this root node C is empty. The right subtree of C is made up of three nodes F, H and I. This is shown in the figure below.

Fig 11.6: Analysis of a binary tree

Now we apply the same recursive definition on the level below the node C. Now the right subtree of the node C will be considered as a tree. The root of this tree is the node F. The left and right subtrees of this root F are the nodes H and I respectively.

The following figure depicts this.

Fig 11.7: Analysis of a binary tree

We make (draw) a tree by joining different nodes with lines. But we cannot join any nodes whichever we want to each other. Consider the following figure.

Fig 11.8: A non-tree structure

It is the same tree, made earlier with a little modification. In this figure we join the node G with D. Now this is not a tree. It is due to the reason that in a tree there is always one path to go (from root) to a node. But in this figure, there are two paths (tracks) to go to node G. One path is from node A to B, then B to D and D to G. That means the path is A-B-D-G. We can also reach to node G by the other path that is the path A-B-E-G. If we have such a figure, then it is not a tree. Rather, it may be a graph. We will discuss about graphs at the end of this course.

Similarly if we put an extra link between the nodes A and B, as in the figure below, then it is also no more a tree. This is a multiple graph as there are multiple (more than 1) links between node A and B.

Fig 11.9: A non-tree structure

Similarly if we put other links between different nodes, then the structure thus developed will not be a tree. The following figure is also an example of a structure that is not a tree as there are multiple links between the different nodes.

Fig 11.10: A non-tree structure

Terminologies of a binary tree

Now let’s discuss different terminologies of the binary tree. We will use these terminologies in our different algorithms. Consider the following figure.

Fig 11.11: Terminologies used in a binary tree

We have discussed that the node on the top is said root of the tree. If we consider the relationship of these nodes, A is the parent node with B and C as the left and right descendants respectively. C is the right descendant of A. Afterwards, we look at the node B where the node D is its left descendant and E is its right descendant. We can use the words descendant and child interchangeably. Now look at the nodes D, G, H and I. These nodes are said leaf nodes as there is no descendant of these nodes. We are just introducing the terminology here. In the algorithms, we can use the words root or parent, child or descendant. So the names never matter.

Strictly Binary Tree

There is a version of the binary tree, called strictly binary tree. A binary tree is said to be a strictly binary tree if every non-leaf node in a binary tree has non-empty left and right subtrees.

Now consider the previous figure 11.11. We know that a leaf node has no left or right child. Thus nodes D, G, H and I are the leaf nodes. The non-leaf nodes in this tree are A, B, C, E and F. Now according to the definition of strictly binary tree, these non-leaf nodes (i.e. A, B, C, E and F) must have left and right subtrees (Childs). The node A has left child B and right child C. The node B also has its left and right children that are D and E respectively. The non-leaf node C has right child F but not a left one. Now we add a left child of C that is node J. Here C also has its left and right children. The node F also has its left and right descendants, H and I respectively. Now the last non-leaf node E has its left child, G but no right one. We add a node K as the right child of the node E. Thus the tree becomes as shown below in the figure 11.12.

Fig 11.12: A Strictly binary tree

Now all the non-leaf nodes (A, B, C, E and F) have their left and right children so according to the definition, it is a strictly binary tree.

Level

The level of a node in a binary tree is defined as follows:

· Root has level 0,

· Level of any other node is one more than the level its parent (father).

· The depth of a binary tree is the maximum level of any leaf in the tree.

To understand level of a node, consider the following figure 11.13. This figure shows the same tree of figure 11.2, discussed so far.

0 ---------------------------------------- Level 0 1 1 ------------------- Level 1 2 2 2 ------- Level 2 3 3 3 -Level 3 Fig 11.13: Level of nodes of a tree

In the above figure, we have mentioned the level of each node. The figure also shows that the root node has level 0. We have talked in the definition of the level that the level of a node, other than root, is one more than the level of its parent. Now in the tree, the parent of nodes B and C is node A with level 0. Now by definition, the level of B and C will be 1 (i.e. level of A + 1). Now if go downward in the tree and see the nodes D, E and F, the parent node of D and E is B the level of which is 1. So the level of D and E is 2 (i.e. 1 + 1). Similarly the level of F is 2 as the level of its parent (i..e. C) is 1. In the same way, we can easily understand that the level of G, H and I is 3 as the parent nodes of these (E and F) have level 2. Thus we see that tree has multi levels in the downward direction. The levels of the tree increase, as the tree grows downward more. The number of nodes also increases.

Now let’s talk why we call it a binary tree. We have seen that each node has a maximum of two subtrees. There might be two, one or no subtree of a node. But it cannot have more than two. So, we call such a tree a binary one due to the fact that a node of it can have a maximum of two subtrees. There are trees whose nodes can have more than two subtrees. These are not binary trees. We will talk about these trees later.

By seeing the level of a tree, we can tell the depth of the tree. If we put level with each node of the binary tree, the depth of a binary tree is the maximum level. In the figure 11.13, the deepest node is at level 3 i.e. the maximum level is 3. So the depth of this binary tree is 3.

Complete Binary Tree

Now, if there are left and right subtrees for each node in the binary tree as shown below in figure 11.14, it becomes a complete binary tree.

0 1 1 2 2 2 2 3 3 3 3 3 3 3 3 Fig 11.14: A Complete Binary Tree

The definition of the complete binary tree is

“A complete binary tree of depth d is the strictly binary tree all of whose leaves are at level d”.

Now look at the tree, the leaf nodes of the tree are at level 3 and are H, I, J, K, L, M, N and O. There is no such a leaf node that is at some level other than the depth level d i.e. 3. All the leaf nodes of this tree are at level 3 (which is the depth of the tree i.e. d). So this is a complete binary tree. In the figure, all the nodes at level 3 are highlighted.

We know that the property of the binary tree is that its node can have a maximum of two subtrees, called as left and right subtrees. The nodes increase at each level, as the tree grows downward. In a complete binary tree, the nodes increase in a particular order. If we reconsider the previous tree (figure 11.14), we note that the number of node at level 0 is 1. We can say it 2⁰, as 2⁰ is equal to 1. Down to this, the node is the level 1 where the number of nodes is 2, which we can say 2¹, equal to 2. Now at the next level (i.e. level 2), the number of nodes is 4 that mean 2². Finally the number of nodes at level 3 is 8, which can be called as 2³. This process is shown pictorially in the following figure 11.15.

------------- Level 0: 20 nodes ---------- Level 1: 21 nodes ---------- -------------- Level 2: 22 nodes ----------------- - ------------------------------------ Level 3: 23 nodes -------------------------------------------- Fig 11.15: Number of nodes at each level in a complete binary tree

By observing the number of nodes at a particular level, we come to the conclusion that the number of nodes at a level is equal to the level number raising to the power of two. Thus we can say that in a complete binary tree at a particular level k, the number of nodes is equal to 2^k. Note that this formula for the number of nodes is for a complete binary tree only. It is not necessary that every binary tree fulfill this criterion. Applying this formula to each level while going to the depth of the tree (i.e. d), we can calculate the total number of nodes in a complete binary tree of depth d by adding the number of nodes at each level. This can be written as the following summation.

20+ 21+ 22 + ……… + 2d = S^d _j=0 2j = 2d+1 – 1

Thus according to this summation, the total number of nodes in a complete binary tree of depth d will be 2d+1 – 1. Thus if there is a complete binary tree of depth 4, the total number of nodes in it will be calculated by putting the value of d equal to 4. It will be calculated as under.

2⁴⁺¹ - 1 = 2⁵ – 1 = 32 – 1 = 31

Thus the total number of nodes in the complete binary tree of depth 4 is 31.

We know that the total number of nodes (leaf and non-leaf) of a complete binary tree of depth d is equal to 2d+1 – 1. In a complete binary tree, all the leaf nodes are at the depth level d. So the number of nodes at level d will be 2^d . These are the leaf nodes. Thus the difference of total number of nodes and number of leaf nodes will give us the number of non-leaf (inner) nodes. It will be (2d+1 – 1) – 2^d i.e. 2^d – 1. Thus we conclude that in a complete binary tree, there are 2^d leaf nodes and 2^d – 1 non-leaf (inner) nodes.

Level of a Complete Binary Tree

We can conclude some more results from the above mathematical expression. We can find the depth of a complete binary tree if we know the total number of nodes. If we have a complete binary tree with n total nodes, then by the equation of the total number of nodes we can write

Total number of nodes = 2d+1 – 1 = n

To find the value of d, we solve the above equation as under

2d+1 – 1 = n

2d+1 = n + 1

d + 1 = log₂ (n + 1)

d = log₂ (n + 1) – 1

After having n total nodes, we can find the depth d of the tree by the above equation. Suppose we have 100,000 nodes. It means that the value of n is 100,000, reflecting a depth i.e. d of the tree will be log₂ (100000 + 1) – 1, which evaluates to 20. So the depth of the tree will be 20. In other words, the tree will be 20 levels deep. The significance of all this discussion about the properties of complete binary tree will become evident later.

Technorati Tags: ds tutorial,data structure tutorial,tree data structure,trees in data structure,tree ds,tree traversal data structure,tree types,types of trees,binary trees,binary search trees,bst,bst data structure,bst ds,complete binary search tree,non tree structure,linear tree,complete binary tree

Uses of Queues

Out of the numerous uses of the queues, one of the most useful is simulation. A simulation program attempts to model a real-world phenomenon. Many popular video games are simulations, e.g., SimCity, Flight Simulator etc. Each object and action in the simulation has a counterpart in the real world. Computer simulation is very powerful tool and it is used in different high tech industries, especially in engineering projects. For example, it is used in aero plane manufacturing. Actually Computer Simulation is full-fledged subject of Computer Science and contains very complex Mathematics, sometimes. For example, simulation of computer networks, traffic networks etc.

If the simulation is accurate, the result of the program should mirror the results of the real-world event. Thus it is possible to understand what occurs in the real-world without actually observing its occurrence.

Let us look at an example. Suppose there is a bank with four tellers.

A customer enters the bank at a specific time (t₁) desiring to conduct a transaction.

Any one of the four tellers can attend to the customer. The transaction (withdraws, deposit) will take a certain period of time (t₂). If a teller is free, the teller can process the customer’s transaction immediately and the customer leaves the bank at t₁+t₂. It is possible that none of the four tellers is free in which case there is a line of customers at each teller. An arriving customer proceeds to the back of the shortest line and waits for his turn. The customer leaves the bank at t₂ time units after reaching the front of the line.

The time spent at the bank is t₂ plus time waiting in line.

So what we want to simulate is the working environment of the bank that there are specific number of queues of customers in the bank in front of the tellers. The tellers are serving customers one by one. A customer has to wait for a certain period of time before he gets served and by using simulation tool, we want to know the average waiting time of a bank customer. We will talk about this simulation in the next lecture and will do coding also in order to understand it well.

Suppose, customers want to deposit or withdraw money from a bank, having four cashiers or tellers. The teller helps you in depositing the money or withdrawing the money from the same window. This window is known as teller window. The customer needs some service from the bank like depositing the money, bill etc. This transaction needs some time that may be few minutes. A person enters the bank and goes to the teller who is free and requests him to do the job. After the completion of the transaction, the person goes out of the bank. Now we will discuss a scenario when there is a lot of rush of customers. The tellers are just four. Now the tellers are busy and the new customers will form a queue. In this example, we need a queue in front of each of the tellers. A new customer enters the bank and analyzes the four queues and wants to join the shortest queue. This person has to wait for the persons in front of him to be served. Another person may come behind him. In this simulation, we will restrict the person from changing the queue. A person comes into the bank at 10 O clock. His transaction time is 5 minutes. He has to wait for another fifteen minutes in the queue. After this, the teller serves him in 5 min. This person comes at 10 am and waits for fifteen minutes. As the transaction time is 5 minutes, so he will leave the bank at 1020. Now this is the situation of simulation and we have to write a program for this. We can go to some bank and analyze this situation and calculate the time. At the end of the day, we can calculate the average time for each of the customer. This time can be 30 minutes. Here we will simulate this situation with the help of a computer program. This is the real life example. Let’s see the picture of simulations to understand what is happening in the bank.

In the picture below, we have four tellers and four queues, one for each of the tellers. Each teller is serving a customer. When the transaction of a customer is completed, he will leave the bank.

A person enters the bank. He sees that all the four tellers are busy and in each queue there are two persons waiting for their turn. This person chooses the queue no. 3. Another person enters the bank. He analyzed all the queues. The queue no 3 is the biggest and all other are having 2 persons in the queue. He chooses the queue no 1.

Now we have three persons waiting in queue no 1 and 3 and two persons waiting in queue no 2 and 4. The person in queue no.1 completes his transaction and leaves the bank. So the person in the front of the queue no. 1 goes to the teller and starts his transaction. Similarly the person at queue No. 3 finishes his transaction and leaves the premises. The person in front of queue number 3 goes to the teller.

Another person enters the bank and goes to the queue No. 1. This activity goes on. The queues become bigger and shorter. The persons coming in the bank have to wait. If the queues are shorter, people have to wait for less time. However, if the queues are longer, people have to wait for more time. The transactions can also take much more time, keeping the people waiting. Suppose four persons come with big amount and their transaction takes too much time. These are all parameters which we can incorporate in our simulation making it real. For this, we have carry out more programming. With the introduction of these parameters in the simulation, it will be more close to the real life situation. Simulation, being a very powerful technique, can yield the results, very close to some real life phenomenon.
Simulation Models

Let’s discuss little bit about the simulation models. Two common models of simulation are time-based simulation and event-based simulation. In time-based simulation, we maintain a timeline or a clock. The clock ticks and things happen when the time reaches the moment of an event.

Suppose we have a clock in the computer. The minute hand moves after every minute. We know the time of the customer’s entry into the bank and are aware that his transaction takes 5 minutes. The clock is ticking and after 5 minutes, we will ask the customer to leave the bank. In the program, we will represent the person with some object. As the clock continues ticking, we will treat all the customers in this way. Note that when the customer goes to some teller, he will take 5 minutes for his transaction. During this time, the clock keeps on ticking. The program will do nothing during this time period. Although some other customer can enter the bank. In this model, the clock will be ticking during the transaction time and no other activity will take place during this time. If the program is in some loop, it will do nothing in that loop until the completion of the transaction time.

Now consider the bank example. All tellers are free. Customer C1 comes in 2 minutes after the opening of the bank. Suppose that bank opens at 9:00 am and the customer arrives at 9:02 am. His transaction (withdraw money) will require 4 minutes. Customer C2 arrives 4 minutes after the bank opens (9:04 am). He needs 6 minutes for transaction. Customer C3 arrives 12 minutes after the bank opens and needs 10 minutes for his transaction.

We have a time line and marks for every min.

C1 comes at 2 min, C2 enters at 4 min. As C1 needs 4 min for his transaction, so he leaves at 6 min. C2 requires 6 min for the processing so C2 leaves at 10 min. Then C3 enters at 12 min and so on. This way, the activity goes on. Therefore, we can write a routine of the clock. We take a variable clock representing the clock. The clock will run for 24 hrs. Banks are not open for 24 hrs but we will run our loop for 24 hrs. The pseudo code is as under:

clock = 0; while ( clock <= 24*60 ) { // one day read new customer; if customer.arrivaltime == clock insert into shortest queue; check the customer at head of all four queues. if transaction is over remove from queue. clock = clock + 1; }

The variable clock is initialized to zero. The while loop runs for 24 hrs. Then we read a new customer. This information may be coming from some file. The if statement is checking the arrival time of the customer. He comes 10 minutes after the opening of the bank. So when this time is equal to the clock, we insert the customer in the shortest queue. Then we will check the transaction time of all the four customers at each teller. If the transaction time of any customer ends, we will remove it from the queue and he will leave the bank. In the end, we increment the clock with one minute. As seen in the above statements, some activity takes place when the clock reaches at the event time (that is the time to enter the bank or leave the bank arrives). If the customer’s arrival time has not come, the first if statement becomes false and we do nothing. Similarly if the transaction of customer is not finished, the second if statement becomes false. Then this while loop will simply add one min to the clock. This is the clock- based (time- based) simulation.

Let’s discuss the other type of simulation i.e. the event-based simulation. Don’t wait for the clock to tick until the next event. Compute the time of next event and maintain a list of events in increasing order of time. Remove an event from the list in a loop and process it. Let’s see the time line again.

The customer C1 comes at 2 min and leaves at 6 min. Customer C2 comes at 4 min and leaves at 10 min and so on. We have written the events list in the above figure. Do not see the clock but see the events on time. Event 1 occurs at 2 min that is the customer C1 enters the bank 2 minutes after its opening. Event 2 is that C2 enters at 4 min. Event 3 is that the customer C1 leaves the bank at 6 min. Event 4 is that the C2 leaves the bank at 10 min and event 5 is that C3 enters the bank at 12 min. Here we have a list of events. How can we process them? We will make a queue of these events. Remove the event with the earliest time from the queue and process it. Insert the newly created events in the queue. A queue where the de-queue operation depends not on FIFO, is called a priority queue.

Technorati Tags: data structure tutorial,ds tutorial,queues,priority queues,priority queues implementation,priority queue data structure,priority queue simulation,priority queue example,priority queue,priority queue tutorial,uses of queues,queue uses