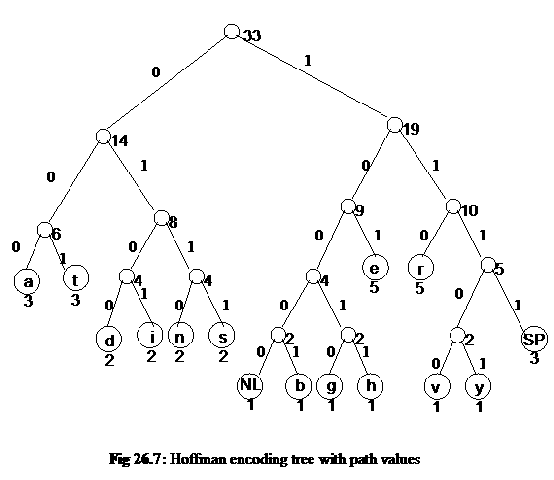
There is a relationship between internal nodes and external nodes i.e. If the number of internal nodes is N, the number of external nodes will be N+1. Let us discuss another property of the binary trees.
Property
A binary tree with N internal nodes has 2N links, N-1 links to internal nodes and N+1 links to external nodes.
Please recall that the first property dealt with the relationship between internal and external nodes. This property is dealing with the relationship of links to the internal nodes.
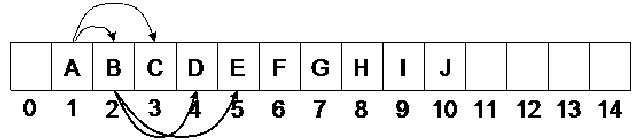
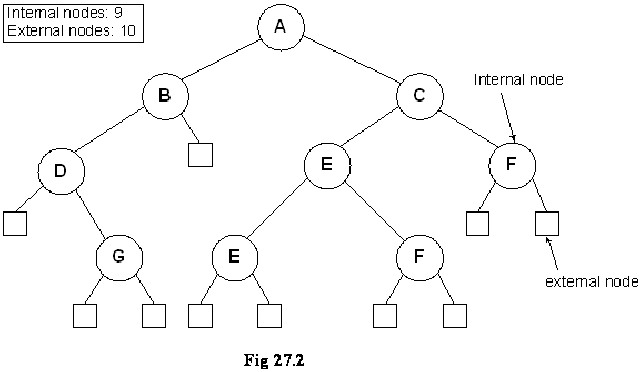
Now, what is a link? As you might already have understood, a link is that line, which we draw between two nodes in a tree. Internally we use pointers in C++ to realize links. In pictorial sketches, however, we use a line to show a link between the two nodes. The property defines, that if you have a binary tree with Nodes, how many links, it will have between the internal nodes (remember, it includes the leaf nodes), and how many links it will have between the external nodes. We have not been showing any links between the external nodes in the diagrams. These are, in fact, null pointers. That means, these are the links, which we will show with the help of the square nodes. Let us see a binary tree, on the basis of which, we will further explore this property. In the following figure, the binary tree is shown again, which, in addition to the normal links between the internal nodes, also contains external nodes as squares and the external links as lines going to those squares.
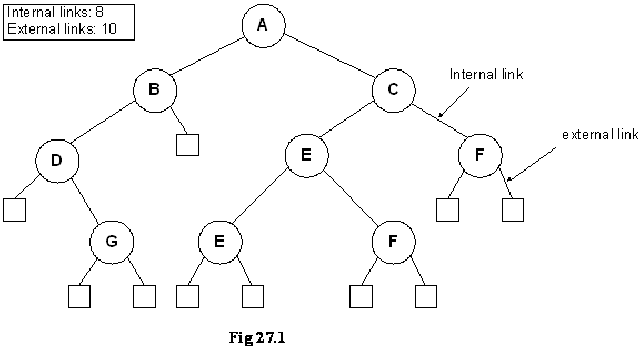
Now if you count the total number of links in the diagram between internal and external nodes, it will be 2N. Remember, we are talking about links and not nodes. In this tree, we have 9 nodes marked with capital letters, 8 internal links and 10 external links. Adding the both kinds of links, we get 18, which is exactly 2 x 9.
As discussed already that these properties are mathematical theorems and can therefore be proven mathematically. Let us now prove this property as to how do we get 2N links in a binary tree with N internal nodes.
Property
A binary tree with N internal nodes has 2N links, N-1 links to internal nodes and N+1 links to external nodes.
- In every rooted tree, each node, except the root, has a unique parent.
- Every link connects a node to its parents, so there are N-1 links connecting internal nodes.
- Similarly each of the N+1 external nodes has one link to its parents.
- Thus N-1+N+1=2N links.
In the previous lectures, I told you about the important property of the trees, that they contain only one link between the two nodes. I had also shown you some structures, which did not follow this property and I told you, that those were graphs.
Threaded Binary Trees
- In many applications binary tree traversals are carried out repeatedly.
- The overhead of stack operations during recursive calls can be costly.
- The same would true if we use a non-recursive but stack-driven traversal procedure
- It would be useful to modify the tree data structure which represents the binary tree so as to speed up, say, the inorder traversal process: make it "stack-free".
You must be remembering that there were four traversing methods of binary trees: preorder, inorder,
postorder and levelorder. First three preorder, inorder and postorder were implemented using recursion. Those recursive routines were very small, 3 to 4 lines of code and they could be employed to traverse a tree of any size.
We also traversed BST in inorder to retrieve the information in sorted order. We employed stacks in recursive implementations. Although, recursive routines are of few lines but when recursion is in action, recursive stack is formed that contains the function calls. We also explicitly used stack for inorder non-recursive traversal. When the calling pattern of recursive and non-recursive stack based routines were compared, the calling pattern of both of the routines were similar.
Suppose that we have a BST that is traversed again and again for some operations of find or print. Due to lot of recursive operations, the stack size keeps on growing. As a result, the performance is affected. To overcome this performance bottleneck, we can use non-recursive method but stack-driven traversal will again be an issue. The push and pop operations of stack for insertion and retrieval will again take time. So is there a way to do traversal without using a stack neither of implicit function call stack nor explicit. The same idea is presented in the last bullets above that leads to threaded binary trees:
- It would be useful to modify the tree data structure which represents the binary tree so as to speed up, say, the inorder traversal process: make it "stack-free".
The idea in the above statement is to modify the tree data structure to speed up and make it stack-free. Now, we see what kind of modification is required in the binary trees.
- Oddly, most of the pointer fields in our representation of binary trees are NULL!
- Since every node (except the root) is pointed to, there are only N-1 non-NULL pointers out of a possible 2N (for an N node tree), so that N+1 pointers are NULL.
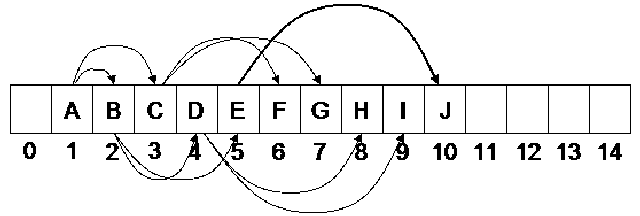
We know that all the leaf node pointers are NULL. Each node of the tree contains the data part, two pointer variables for left and right nodes links. But these pointer variables are used when the node has further child nodes. We know that in a binary tree the total number of links are 2N including both internal and external and the number of NULL pointers is N+1.
In the figure above, the tree is the same as shown in Fig 27.1. The square nodes shown in this figure are external nodes. Thinking in terms of pointers all the pointers of these nodes are NULL or in other words they are available to be used later. We recognize these nodes as leaf nodes. Besides that, what can we achieve using them is going to be covered in Threaded Binary Trees.
- The threaded tree data structure will replace these NULL pointers with pointers to the inorder successor (predecessor) of a node as appropriate.
We are creating a new data structure inside the tree and when the tree will be constructed, it will be called a threaded binary tree. The NULL pointers are replaced by the inorder successor or predecessor. That means while visiting a node, we can tell which nodes will be printed before and after that node.
- We'll need to know whenever formerly NULL pointers have been replaced by non NULL pointers to successor/predecessor nodes, since otherwise there's no way to distinguish those pointers from the customary pointers to children.
This is an important point as we need to modify our previous logic of identifying leaf nodes. Previously the node with left and right nodes as NULL was considered as the leaf node but after this change the leaf node will contain pointers to predecessor and successor. So in order to identify that the pointers has been modified to point to their inorder successor and predecessor, two flags will be required in the node. One flag will be used for successor and other for predecessor. If both the pointers were NULL, left pointer variable will be used to point inorder predecessor, the flag for this will be turned on and the right pointer variable will be used to keep inorder successor and the flag will be turned on once the successor address is assigned.
Adding Threads During Insert
If we print the above tree in inorder we will get the following output:
14 15 18 20
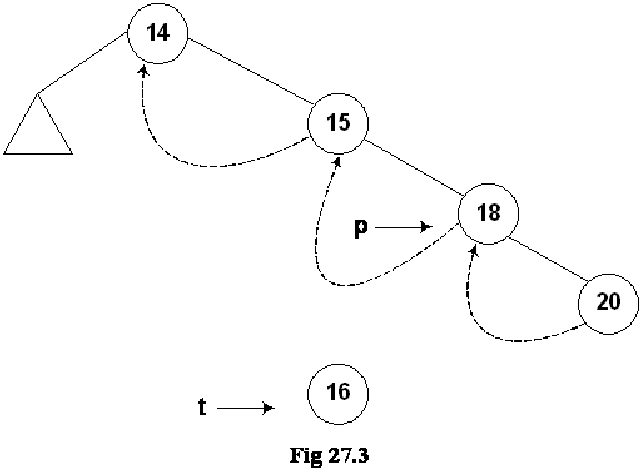
In the above figure, the node 14 contains both left and right links. The left pointer is pointing to a subtree while the right subtree is pointing to the node 15. The node 15’s right link is towards 18 but the left link is NULL but we have indicated it with a rounded dotted line towards 14. This indicates that the left pointer points to the predecessor of the node.
Below is the code snippet for this logic.
t->L = p->L; // copy the thread
t->LTH = thread;
t->R = p; // *p is successor of *t
t->RTH = thread;
p->L = t; // attach the new leaf
p->LTH = child;
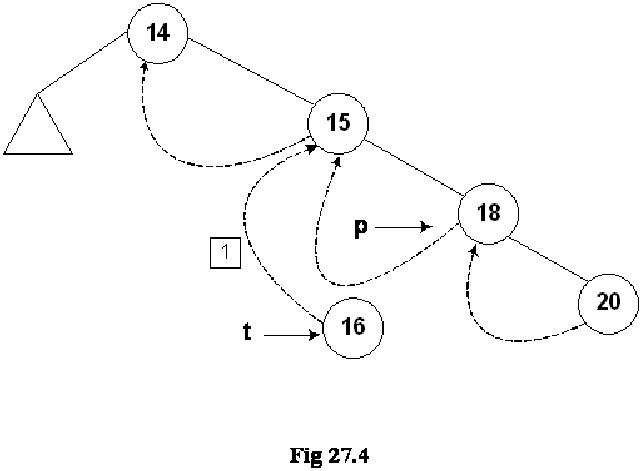
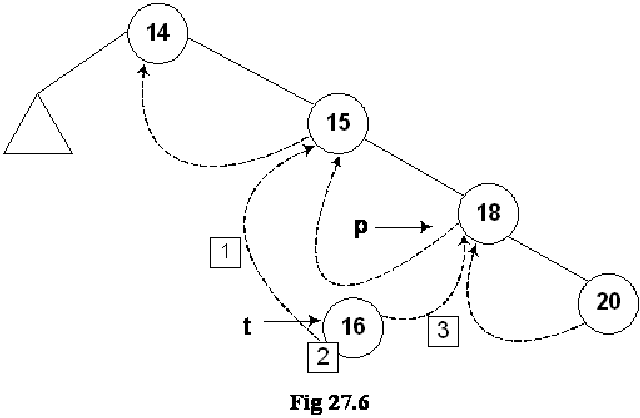
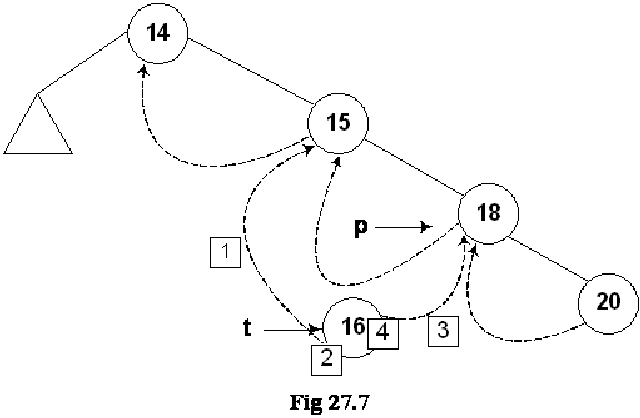
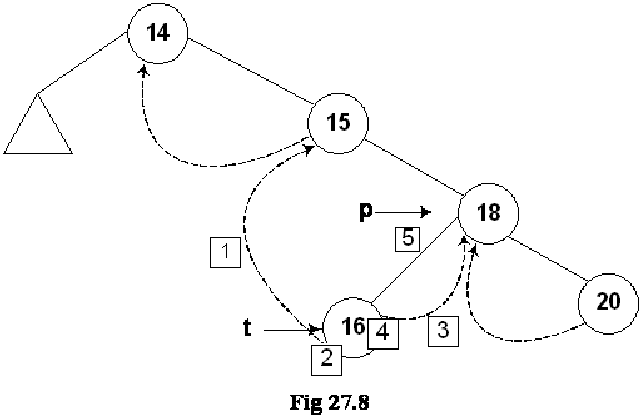
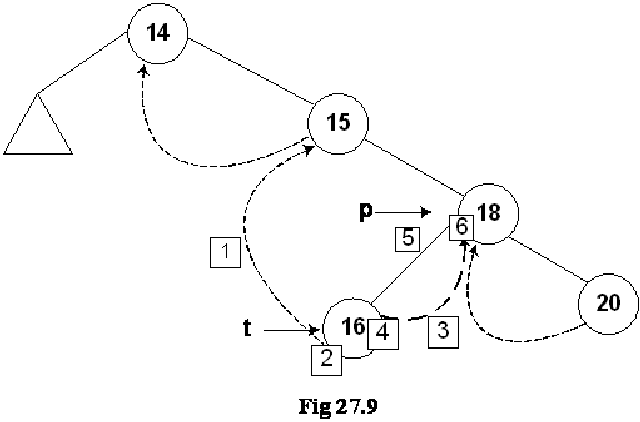
Let’s insert a new node in the tree shown in the above figure. The Fig 27.4 indicates this new insertion.
The new node 16 is shown in the tree. The left and right pointers of this new node are NULL. As node 16 has been created, it should be pointed to by some variable. The name of that variable is t. Next, we see the location in the tree where this new node with number 16 can be inserted. Clearly this will be after the node 15 but before node 18. As a first step to insert this node in the tree as the left child of the node 18, we did the following:
1. t->L = p->L; // copy the thread
2. t->LTH = thread;
3. t->R = p; // *p is successor of *t
4. t->RTH = thread;
5. p->L = t; // attach the new leaf
6. p->LTH = child;
As the current predecessor of node 18 is 15. After node 16 will be inserted in the tree, it will become the inorder predecessor of 18, therefore, in the first line of the code t->L = p->L, left pointer of node 18 (pointed to by pointer p) is assigned to the left pointer of node 16 (pointer to by pointer t).
In the next line of code t->LTH = thread, the left flag is assigned a variable thread that is used to indicate that it is on.
In the third line of code, t->R = p, 18 being the successor of node 18, its pointer p is assigned to the right pointer (t->R) of node 16.
Next line, t->RTH = thread contains flag turning on code.
In the next line p->L = t, the node 16 is attached as the left child of the node 18.
The flag is truned on in the last line, p->LTH = child.
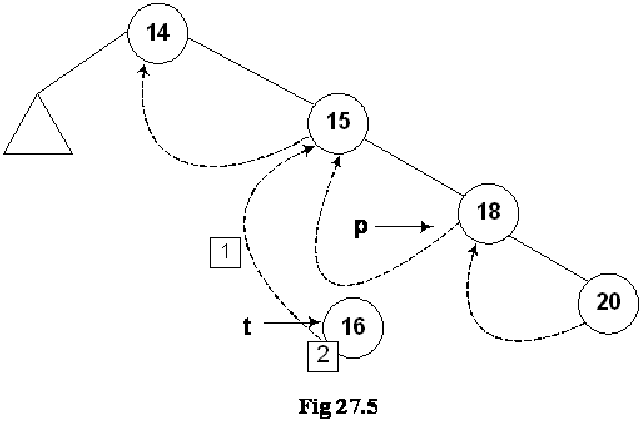
If we insert few more nodes in the tree, we have the tree as given below:
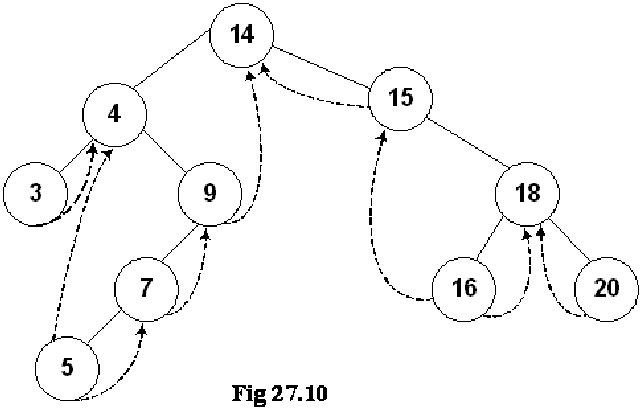
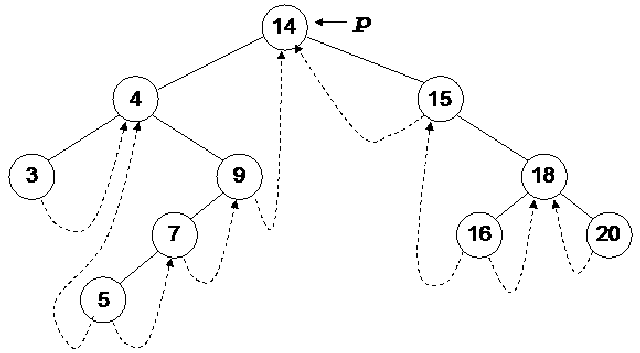
Above given is a BST and you have seen many BSTs before, which are not thread binary trees. Without the threads, it is clear from the figure that there are number of links present in the tree that are NULL. We have converted the NULLs to threads in this tree.
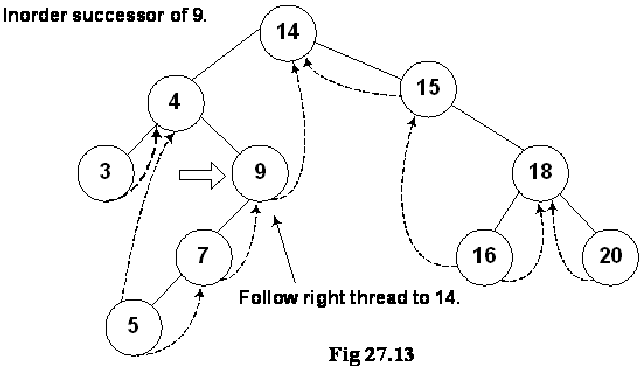
Let’s do inorder non-recursive traversal of the tree. We started at 14 then following the left link came to 4 and after it to 3. If we use recursion then after the call for node 3 is finished (after printing 3), it returns to node 4 call and then 4 is printed using the recursive call stack. Here we will print 3 but will not stop. As we have used threads, we see the right pointer of node 3 that is not NULL and pointing to its successor node 4, we go to 4 and print it. Now which node is inorder successor of node 4. It is node 5.
From node 4, we traversed to right child of it node 9. From node 9, we went to node 7 and then finally node 5. Now, this node 5 is a leaf node. Previously, without using threads, we could identify leaf nodes, whose both pointers left and right were NULL. In this case, using threads, as discussed above, we set the pointers and turn the flags on when a pointer left or right is set to its predecessor or successor. After printing node 5, we traverse its right thread and go to node 7. In this fashion, whole of the tree can be traversed without recursion.
Now, let’s see some code:
TreeNode* nextInorder(TreeNode* p)
{
if(p->RTH == thread)
return(p->R);
else {
p = p->R;
while(p->LTH == child)
p = p->L;
return p;
}
}
Above given is a routine nextInorder, which gives the inorder
successor of a node passed in parameter pointer p. Now what it does is:
If the RTH flag of the p node (the node passed in the parameter) is thread then it will return the node being pointed by the right thread (p->R), which would be its inorder successor. Otherwise, it does the following.
It goes to the right node of p and starts pointing it using the same p pointer. From there it keeps on moving (in a loop fashion) towards the left of the node as long as the statement p->LTH == child is true. After this loop is terminated, the node p is returned.
Next, we see this pictorially.
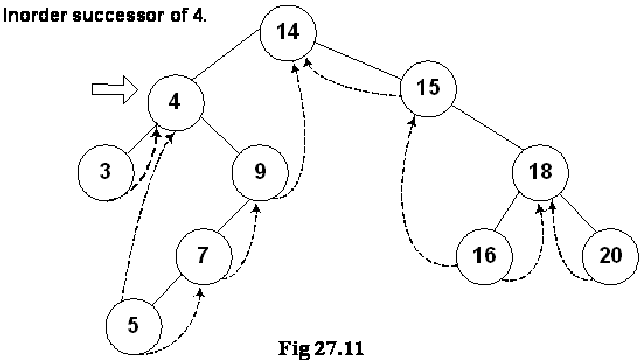
Where is Inorder Successor?
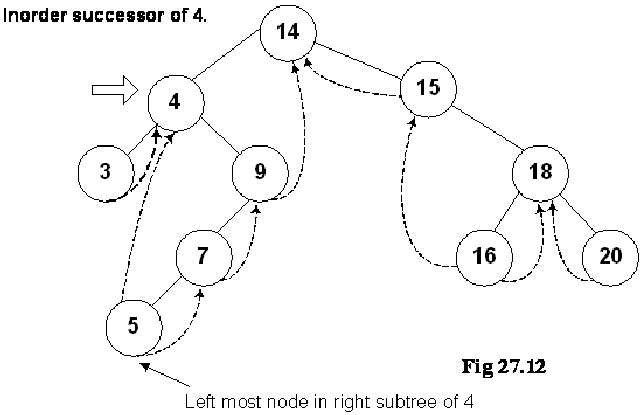
We are at node 4 and want to find its inorder successor. If you remember the delete operation discussed in the previous lecture, where we searched for the inorder successor and found it to be the left-most node in the right subtree of the node.
In this figure, the right subtree of 4 is starting from node 9 and ending at node 5. Node 5 is the left most node of it and this is also the inorder successor of node 4. We cannot go to node 5 directly from node 4, we go to node 9 first then node 7 and finally to node 5.
We move from node 9 to node 5 following the normal tree link and not thread. As long as the normal left tree link is there of a node, we have set the LTH flag to child. When we reach at node 5, the left link is a thread and it is indicated with a flag. See the while loop given in the above routine again:
while(p->LTH == child)
p = p->L;
return p;
Inorder Traversal
Now by using this routine, we try to make our inorder traversal procedure that is non-recursive and totally stack free.
If we can get things started correctly, we can simply call nextInorder repeatedly (in a simple loop) and move rapidly around the tree inorder printing node labels (say) - without a stack.
The pointer p is pointing to the root node of the tree. If we start traversing from this node and pass this root node pointer to our routine nexInorder above, it will create a problem.
We see the routine again to see the problem area clearly:
TreeNode* nextInorder(TreeNode* p)
{
if(p->RTH == thread)
return(p->R);
else {
p = p->R;
while(p->LTH == child)
p = p->L;
return p;
}
}
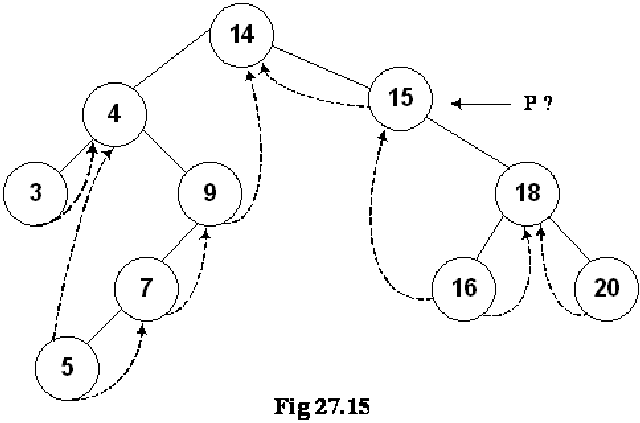
In the first part, it is checking for the RTH flag to be set to thread, which is not the case for the root node. The control will be passed to the else part of the routine. In else part, in the very first step, we are moving towards right of root that is to node 15.
If we call nextInorder with the root of the binary tree, we're going to have some difficulty. The code won't work at all the way we want.
Note that in this tree inorder traversal, the first number we should print is 3 but now we have reached to node 15 and we don’t know how can we reach node 3. This has created a problem. In the lecture, we will make a small change in this routine to cater to this situation i.e. when a root node pointer is passed to it as a parameter. After that change the routine will work properly in case of root node also and it will be non-recursive, stack free routine to traverse the tree.
Inorder traversal in threaded trees
We have introduced the threads in the tree and have written the nextInorder routine. It is sure that the provision of the root can help this routine perform the inorder routine properly. It will go to the left most node before following the threads to find the inorder successors. The code of the routine is given below:
/* The inorder routine for threaded binary tree */
TreeNode* nextInorder(TreeNode* p){
if(p->RTH == thread) return(p->R);
else {
p = p->R;
while(p->LTH == child)
p = p->L;
return p;
}
} |
When we apply this routine on the sample tree, it does not work properly because the pointer that points to the node goes in the wrong direction. How can we fix this problem? Let’s review the threaded binary tree again:
In the above figure, we have a binary search tree. Threads are also seen in it. These threads points to the successor and predecessor.
Our nextInoder routine, first of all checks that the right pointer of the node is thread. It means that it does not point to any tree node. In this case, we will return the right pointer of the node as it is pointing to the inorder successor of that node. Otherwise, we will go to some other part. Here we will change the value of pointer p to its right before running a while loops as long as the left pointer is the node. That means the left child is not a thread. We move to the left of the pointer p and keep on doing so till the time the left pointer becomes a thread.
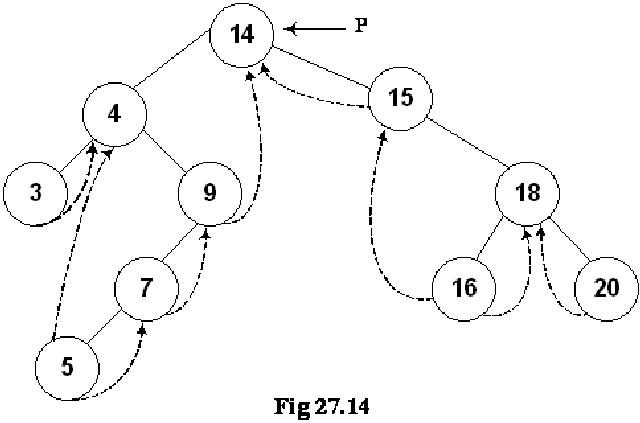
We will pass the root of the tree to the nextInorder routine. The pointer p is pointing to the node 14 i.e. the root node. As the right pointer of the node 14 is not a thread, so the pointer p will move to the node 15 as shown below:
Here we want the inorder traversal. It is obvious from the above figure that 15 is not the first value. The first value should be 3. This means that we have moved in the wrong direction. How this problem can be overcome? We may want to implement some logic that in case of the root node, it is better not to go towards the right side. Rather, the left side movement will be appropriate. If this is not the root node, do as usual. It may lend complexities to our code. Is there any other way to fix it? Here we will use a programming trick to fix it.
We will make this routine as a private member function of the class so other classes do not have access to it. Now what is the trick? We will insert a new node in the tree. With the help of this node, it will be easy to find out whether we are on the root node or not. This way, the pointer p will move in the correct direction.
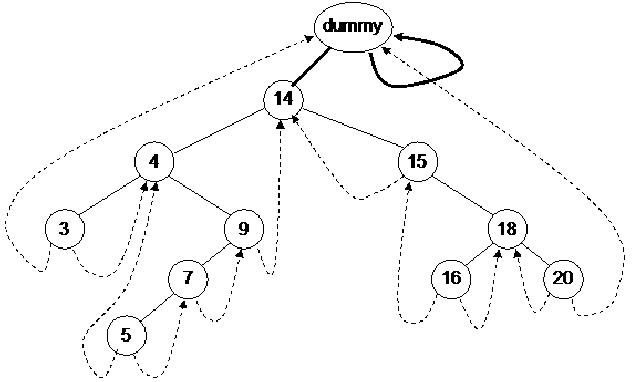
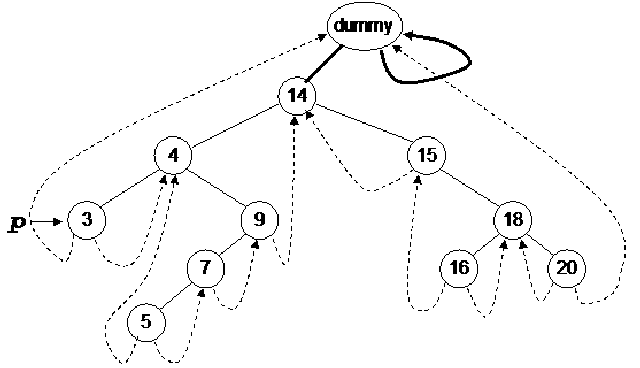
Let’s see this trick. We will insert an extra node in the binary tree and call it as a dummy node. This is well reflected in the diagram of the tree with the dummy node. We will see where that dummy node has been inserted.
This dummy node has either no value or some dummy value. The left pointer of this node is pointing to the root node of the tree while the right pointer is seen pointing itself i.e. to dummy node. There is no problem in doing all these things. We have put the address of dummy node in its right pointer and pointed the left thread of the left most node towards the dummy node. Similarly the right thread of the right-most node is pointing to the dummy node. Now we have some extra pointers whose help will make the nextInorder routine function properly.
Following is a routine fastInorder that can be in the public interface of the class.
/* This routine will traverse the binary search tree */
void fastInorder(TreeNode* p)
{
while((p=nexInorder(p)) != dummy) cout << p->getInfo();
} |
This routine takes a TreeNode as an argument that make it pass through the root of the tree. In the while loop, we are calling the nextInorder routine and pass it p. The pointer returned from this routine is then assigned to p. This is a programming style of C. We are performing two tasks in a single statement i.e. we call the nextInorder by passing it p and the value returned by this routine is saved in p. Then we check that the value returned by the nextInorder routine that is now actually saved in p, is not a dummy node. Then we print the info of the node. This function is called as:
fastInorder(dummy);
We are not passing it the root of the tree but the dummy node. Now we will get the correct values and see in the diagrams below that p is now moving in the right direction. Let’s try to understand this with the help of diagrams.
First of all we call the nextInorder routine passing it the dummy node.
The pointer p is pointing to the dummy node. Now we will check whether the right pointer of this node is not thread. If so, then it is advisable to move the pointer towards the right pointer of the node. Now we will go to the while loop and start moving on the left of the node till the time we get a node with the left pointer as thread. The pointer p will move from dummy to node 14. As the left pointer of node 14 is not thread so p will move to node 4. Again the p will move to node 3. As the left pointer of p is thread, the while loop will finish here. This value will be returned that is pointing to node 3. The node 3 should be printed first of all regarding the inorder traversal. So with the help of our trick, we get the right information.
Now the while loop in the fastInorder will again call the nextInorder routine. We have updated the value of p in the fastInorder that is now pointing to the node 3. This is shown in the figure below:
According to the code, we have to follow the right thread of the node 3 that is pointing to the node 4. Therefore p is now pointing to the node 4. Here 4 is inorder successor of 3. So the pointer p has moved to the correct node for inorder traversal.
As the right pointer of the node 4 is a link, p will move to node 9. Later, we will go on the left of nodes and reach at the node 5. Looking at the tree, we know that the inorder successor of the node 4 is node 5. In the next step, we will get the node 7 and so on. With the help of threads and links, we are successful in getting the correct inorder traversal. No recursive call has been made so far. Therefore stack is not used. This inorder traversal will be faster than the recursive inorder traversal. When other classes use this routine, it will be faster. We have not used any additional memory for this routine. We are using the null links and putting the values of thread in it. This routine is very simple to understand. In the recursive routines, we have to stop the recursion at some condition. Otherwise, it will keep on executing and lead to the aborting of our program.
Technorati Tags:
ds tutorial,
data structure tutorial,
tree data structure,
trees in data structure,
tree ds,
tree traversal data structure,
tree types,
types of trees,
binary trees,
binary search trees,
bst,
bst data structure,
bst ds,
complete binary search tree,
non tree structure,
linear tree,
properties of trees,
binary tree property
![clip_image001[4] clip_image001[4]](http://lh4.ggpht.com/-u2Lb-zvWCFE/ULBxmsa1mbI/AAAAAAAACFk/ZOAvwzAsJaU/clip_image001%25255B4%25255D_thumb%25255B1%25255D.gif?imgmax=800)
![clip_image002[6] clip_image002[6]](http://lh4.ggpht.com/-g-mEIZnsyK8/ULBxpradq5I/AAAAAAAACF0/IipqDkeGDo4/clip_image002%25255B6%25255D_thumb%25255B1%25255D.gif?imgmax=800)
![clip_image003[6] clip_image003[6]](http://lh3.ggpht.com/-W64LvoZ5GU0/ULBxszSnzVI/AAAAAAAACGE/KUkAGwT3HJc/clip_image003%25255B6%25255D_thumb%25255B1%25255D.gif?imgmax=800)

![clip_image002[5] clip_image002[5]](http://lh6.ggpht.com/-VKGE-15G8f0/ULBuz2Fma0I/AAAAAAAACDE/ToP9T6aVbys/clip_image002%25255B5%25255D_thumb%25255B1%25255D.gif?imgmax=800)
![clip_image004[5] clip_image004[5]](http://lh4.ggpht.com/-iGP8ShJktvY/ULBu6IYDLcI/AAAAAAAACDk/ll1FGkwXFUA/clip_image004%25255B5%25255D_thumb%25255B1%25255D.gif?imgmax=800)
![clip_image001[4] clip_image001[4]](http://lh6.ggpht.com/-2L9MnG6VQ5U/UKk4ahIG2NI/AAAAAAAAB7I/EKM1o6-ttzg/clip_image001%25255B4%25255D_thumb%25255B1%25255D.gif?imgmax=800)
![clip_image002[4] clip_image002[4]](http://lh6.ggpht.com/-OGX49iU8ApE/UKk4diz22sI/AAAAAAAAB7Y/DNVVK1K7hIQ/clip_image002%25255B4%25255D_thumb%25255B1%25255D.gif?imgmax=800)